总体上看,中国房地产市场自1999年开始经历了10多年的长期增长。有关统计资料显示,中国商品房平均价格由1999年的2 053元/m2上升至2008年的3 800元/m2(受国家宏观调控的影响,2008年比上年有所下降),10年间上涨了1.85倍。2009年以后,我国房地产市场再次趋热,北京、上海、广州、杭州等一线城市的房价迭创新高。与此同时,更值得关注的现象是,房地产作为一个特殊的商品,在房价持续走高的同时,其需求依然保持了十分强劲的态势,也就是说,我国房价的上涨并没有抑制市场的需求,相反却刺激了市场购买的欲望。各年份《中国统计年鉴》的数据显示,自2003年起,我国商品房屋销售额增长迅猛,至2009年,商品房屋销售额已高达43 995亿元,这个规模是1999年的15倍。①
与房地产业飞速发展密不可分的是银行信贷资金②的支持。房地产业是一个资金密集型行业,对资金需求量非常大。自1999年以来,房地产开发贷款在房地产开发企业(单位)资金来源中占了20%左右。个别年份如1999年、2003年,房地产开发贷款在房地产开发企业(单位)资金来源占比均为23%,超过了平均水平,而2008年、2009年则分别为19%、20%。③这些数据说明,中国房地产市场对银行资金的依赖非常大,房地产行业聚集了较多的银行资金。
房地产业作为我国的支柱产业,对我国经济增长的贡献是有目共睹的。但是,由于房地产市场的价格、需求与银行信贷之间呈现为错综复杂的关系,一旦因市场过热而引发宏观调控时,政府及其有关监管部门首选的调控措施往往就是对银行信贷施以严格的约束。另一方面,我国近几次对房地产市场的调控大多导致各级政府对经济增长的担忧,各类银行也纷纷采取一些变通的办法规避信贷方面的政策限制。始于2010年4月的新一轮房地产宏观调控,就集中反映了我国房地产市场波动与银行信贷、经济增长之间的矛盾状况。可见,为了实现我国房地产市场稳定、健康发展的目标,我们有必要明确:中国房地产市场波动与经济增长到底是什么关系?银行信贷资金对房地产的支持程度究竟如何?
有关中国房地产业发展与经济增长之关系的研究文献不胜枚举。夏丹(2007)选取GDP作为衡量经济发展的数据支持,以房地产开发投资完成额作为房地产业发展的适合量度,运用协整方法对我国房地产行业与经济增长之间的动态均衡关系进行了分析,认为我国房地产行业发展状况对当前GDP变动的影响并不是很显著,房地产行业发展与经济增长之间不存在明显的因果关系。李熙娟、李斌(2006)采用1978—2002年的数据,利用协整检验以及格兰杰因果检验模型,对房地产业发展与国民经济增长之间的协整关系和因果关系分别进行检验,结果表明,两者之间并不存在长期稳定的关系,但是滞后1—3期时,两者互为因果关系。皮舜、武康平(2004)基于面板数据和格兰杰因果检验模型,研究发现1994年到2002年间我国区域房地产市场的发展与经济增长之间存在着双向因果关系。可见,已有文献大多明确了我国房地产业发展与经济增长之间的互动关系,但对于具体影响如何却见仁见智。
一部分文献对中国房地产价格与需求进行了分析。高波、王斌(2008)利用全国35个大中城市1999—2006年的面板数据对房地产市场的需求价格弹性和需求收入弹性进行估计,结果表明,我国房地产需求价格弹性总体上是缺乏弹性的,而收入弹性是富有弹性的。这也解释了为什么在房价不断上涨的同时,房地产市场需求依然不减。有很多学者也对银行信贷与房地产价格之间的关系进行过实证分析。邹朋飞(2008)认为,房地产价格存在明显的双向正反馈效应,信贷规模的增长对房地产价格上涨贡献最大;房地产价格的上涨及上涨预期增强了银行的贷款冲动,刺激了投机需求和地方政府官员的政绩需求,它们共同推动房地产价格和土地交易价格进一步上涨,两者循环作业,最终导致了房地产价格的螺旋式上升。段忠东、曾令华、黄泽先(2007)也认为,房地产价格和银行信贷之间在长期内存在互为因果的关系,房地产价格波动在短期对银行信贷发放的直接影响十分有限,主要是在长期对银行信贷增长产生影响;但是,银行信贷也通过协整关系成为房地产价格短期波动的格兰杰原因。
不过,迄今为止,将房地产市场波动与银行信贷、经济增长三者之间关系纳入同一分析框架的文献却极其有限。李宏瑾(2005)通过建立我国31个省份1999—2003年的静态面板模型,在此方面进行了实证分析,并认为,银行信贷资金对房地产市场供求都起着支持作用,且房地产的供给约束非常严重,在居民收入增长时,无法满足居民的需求,从而致使房价居高不下。这一文献精湛的研究思路为本文提供了有益的借鉴。
本文拟对李宏瑾(2005)所采用的静态面板模型进行一定的修正,试图通过建立动态面板模型,对1999—2008年这10年间中国房地产市场波动与银行信贷、经济增长三者之间的关系作进一步的解释。
二 理论假说在以前的研究文献中,李宏瑾(2005),段忠东、曾令华、黄泽先(2007),邹朋飞(2008)提出房价的波动造成了银行信贷规模的变动。本文则试图通过建立我国31个省份的动态面板模型来验证这一结论。因此,本文提出假说1。
假说1:房地产价格的上升是银行信贷扩张的原因。
房地产业是资金密集型行业,且房地产行业对资金价格是非常敏感的,因而,银行信贷规模和信贷条件对其发展有很大的影响。换句话说,房地产开发贷款在某种程度上会增加房地产供给。因此,本文提出假说2。
假说2:房地产开发贷款与房地产供给成同方向变化。
在我国,房地产业已成为支柱产业。房地产行业的发展促进了与之相关联的上下游产业的发展,如建筑、建材、钢铁、机械、金融等服务业及其他相关部门产业的发展;同时,居民对住房品质的追求又会促进家庭消费品的升级及其需求的扩大;房地产业的发展还间接刺激、带动了城市基础设施的改善和相关公共服务品质的提升。因此,本文提出假说3。
假说3:房地产市场需求的增长将拉动经济的发展。
在以下的分析中,本文将构造相应的模型对上述三个假说进行验证。
三 模型建立 (一) 数据来源与处理本文利用1999年至2008年我国31个省份房地产市场的商品房屋平均销售价格、商品房屋销售额、房地产竣工面积、城镇居民家庭可支配收入、房地产开发贷款和国内生产总值的年度数据,共1 860个样本数据,来分析房地产市场波动与银行信贷、经济增长之间的关系。若无特殊说明,本文的数据均出自于1999—2009年各年份的《中国统计年鉴》。其中,采用“商品房屋销售额”作为代表房地产市场实际需求的变量;采用“房地产竣工面积”来反映房地产市场的实际供给情况(李宏瑾,2005)。
(二) 数据基本特征描述1.1999—2008年房地产价格与银行信贷关系。图 1显示,在样本期内,房地产价格与银行信贷存在着一定的相关性。这也暗示了银行信贷规模与房价波动之间存在着某种联系。
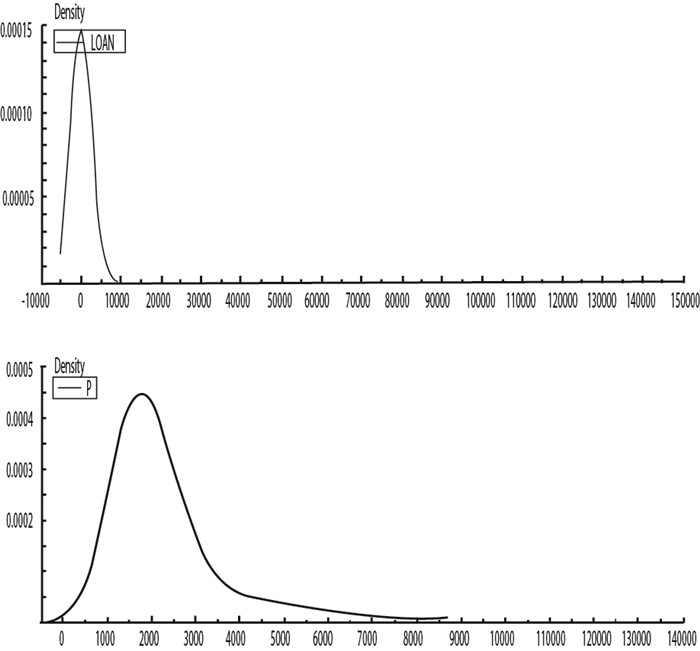
|
图 1 房地产价格与房地产开发贷款分布图 |
2.1999—2008年房地产需求与经济增长的关系。图 2显示,在样本期内,中国房地产市场的发展与经济增长之间存在着正的线性关系,可以简单地认为,房地产市场的扩张推动了中国经济的增长。但是,从样本的分布看,线性关系并非特别明显,这似乎暗示了房地产市场的扩张对中国经济增长的促进作用并没有预期的那么显著。
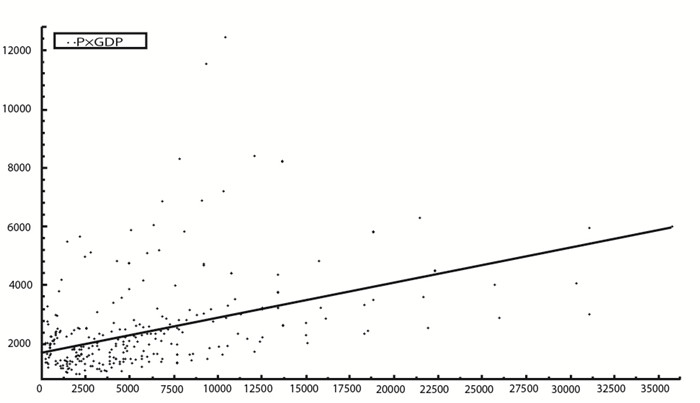
|
图 2 房地产需求与经济增长散点图 |
3.中国房地产市场波动与银行信贷、经济增长的关系。图 3中黑色阴影区域为房地产市场波动与银行信贷、经济增长变化的空间交汇面,这说明,三者之间存在相互关系。结合前文的理论假说,本文认为,房地产市场的扩张刺激了银行的信贷冲动;银行信贷资金流入房地产市场又增加了房地产供给;房地产市场需求的增长促进了经济的增长。对此,下文将作进一步的阐释。
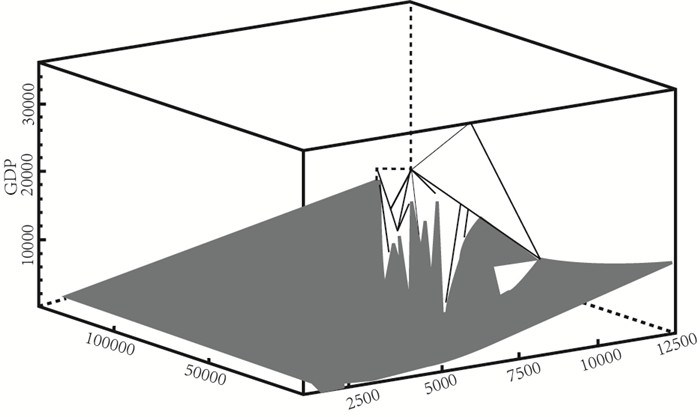
|
图 3 房地产市场扩张、银行信贷与经济增长3D散点图 |
本文采用动态面板数据模型,在模型中增加了自回归项
| $ {{\rm{y}}_{{\rm{it}}}}{\rm{ = }}\sum\limits_{{\rm{k = 1}}}^{\rm{p}} {{{\rm{ \mathsf{ α} }}_{\rm{k}}}{{\rm{y}}_{{\rm{i, t - k}}}}{\rm{ + \mathsf{ β} }}{{\rm{'}}_{{\rm{it}}}}{{\rm{X}}_{{\rm{it}}}}{\rm{ + }}{{\rm{ \mathsf{ λ} }}_{\rm{t}}}{\rm{ + }}{{\rm{ \mathsf{ η} }}_{\rm{i}}}{\rm{ + }}{{\rm{ \mathsf{ ε} }}_{{\rm{it}}}}} $ | (1) |
其中,t=p+1, p+2, …, Ti;i=1, 2, …, N。(1)式中,Xit=(X1it,X2it,…,Xkit)为外生变量;βit′=(β1it′,β2it,…,βkit)为参数向量;K是外生变量的个数;N为截面单位总数;T是时期总数。随机扰动项εit相互独立,且满足零均值、同方差。λ、η为虚拟变量。
(四) 广义矩(GMM)的基本思想在动态面板数据模型中,由于因变量的滞后项作为解释变量,从而有可能导致解释变量与随机扰动项相关,且模型具有横截面相依性(彭建平、李建华,2007),因此,如运用标准随机效应或固定效应模型进行估计,必将产生参数估计的非一致性,使数据包含的经济学意义发生扭曲。正因为如此,Arellano和Bond(1991), Arellano和Bover(1995), Blundell和Bond(1998)有针对性地提出了广义矩(GMM)估计的思路。
GMM假定随机扰动项与一组工具变量不相关,其估计过程就是选择工具变量组与随机扰动项的相关性尽可能为0的参数估计,而该相关性也被定义为准则函数。通过在准则函数中选择适当的加权矩阵,可以使得在未知异方差和自相关形式的情况下,GMM估计依然是稳健的。
假定有一组待估参数θ应满足的理论矩估计条件为:
| $ {\rm{E}}\left( {{{\rm{Z}}^{\rm{'}}}{\rm{u}}\left( {{\rm{y,\theta ,X}}} \right)} \right){\rm{ = 0}} $ | (2) |
(2) 式与Z为一组工具变量,u(y,θ,X)表示一个回归方程的残差。
所谓矩估计,就是用样本矩估计条件去取代理论矩估计条件,即:
| $ \frac{{\sum\limits_{{\rm{i = 1}}}^{\rm{T}} {{{\rm{Z}}^{\rm{'}}}{\rm{u(}}{{\rm{y}}_{\rm{t}}}{\rm{, \mathsf{ θ}, X)}}} }}{{\rm{T}}}{\rm{ = 0}} $ | (3) |
在运用GMM估计时,需要工具变量Z的个数至少要与待估参数向量θ的维数一样。然而,当模型过度识别时,亦即样本矩条件的个数大于参数向量维数时,上述矩条件不是对任何一个参数都满足。此时,参数的矩估计可以通过最小化准则函数
GMM估计的核心思想是运用工具变量产生相应的矩条件方程。为此,首先对方程(1)进行一阶差分,得到方程(4):
| $ \Delta {{\rm{y}}_{{\rm{it}}}}{\rm{ = }}{{\rm{\alpha }}_{\rm{k}}}\Delta {{\rm{y}}_{{\rm{i}},{\rm{t - k - 1}}}}{\rm{ + }}{{\rm{\beta }}^{\rm{'}}}{\rm{it}}\Delta {{\rm{X}}_{{\rm{it}}}}{\rm{ + }}\Delta {{\rm{\lambda }}_{{\rm{it}}}}{\rm{ + \Delta }}{{\rm{\eta }}_{\rm{i}}}{\rm{ + \Delta }}{{\rm{\varepsilon }}_{{\rm{it}}}} $ | (4) |
对方程(1)进行一阶差分的主要目的,在于选取合适的工具变量和产生相应的矩条件方程。由于方程(4)中解释变量αkΔyi, t-k-1与随机项Δεit不相关,此时,可将矩条件设定为:
| $ \begin{array}{l} {\rm{E}}\left({{\rm{f}}\left({\rm{ \mathsf{ α} }} \right)} \right){\rm{ = E}}\left({\sum\limits_{{\rm{i = 1}}}^{\rm{p}} {{{\rm{f}}_{\rm{i}}}\left({\rm{ \mathsf{ α} }} \right)} } \right)\\ {\rm{ = E}}\left({\sum\limits_{{\rm{i = 1}}}^{\rm{p}} {{{\rm{Z}}^{\rm{'}}}_{\rm{i}}{{\rm{ \mathsf{ σ} }}_{\rm{i}}}\left({\rm{ \mathsf{ α} }} \right)} } \right){\rm{ = 0}} \end{array} $ | (5) |
(5) 式中,Zi′即为所选取得Ti×1的工具变量向量,定义残差:
| $ {{\rm{ \mathsf{ σ} }}_{\rm{i}}}\left({\rm{ \mathsf{ α} }} \right){\rm{ = \Delta }}{{\rm{y}}_{{\rm{i, t}}}}{\rm{ - \Delta }}{{\rm{y}}_{{\rm{i, t - 1}}}} $ | (6) |
进而基于残差和工具变量以及加权阵H定义下属目标函数:
| $ {\rm{S}}\left({\rm{ \mathsf{ α} }} \right){\rm{ = }}{\left({\sum\limits_{{\rm{i = 1}}}^{\rm{p}} {{{\rm{Z}}^{\rm{'}}}_{\rm{i}}{{\rm{ \mathsf{ σ} }}_{\rm{i}}}\left({\rm{ \mathsf{ σ} }} \right)} } \right)^{\rm{'}}}{\rm{H}}\left({\sum\limits_{{\rm{i = 1}}}^{\rm{p}} {{{\rm{Z}}^{\rm{'}}}_{\rm{i}}{{\rm{ \mathsf{ σ} }}_{\rm{i}}}\left({\rm{ \mathsf{ α} }} \right)} } \right) $ | (7) |
通过对目标函数(7)进行迭代求其最小值,由此产生参数的GMM估计。
四 计量结果本文运用Pcgive10.0软件对面板数据进行计量分析,分别得到如下结果。
(一) 房地产价格与银行信贷的GMM估计先前很多文献通过房价与银行信贷资金的VAR协整关系得出两者间存在格兰杰因果关系,即银行信贷规模的增长是房价上涨的重要原因(邹朋飞,2008)。本文通过建立我国31个省份的动态面板数据模型,对这一现象进行计量分析,以探讨银行信贷对房地产市场的影响。
本文将房价作为被解释变量,银行信贷资金作为解释变量。对于检验两者间关系应从两方面予以考虑:一是,由于预期的存在,当期房价将受上一年房价波动的影响;二是,上一年房地产开发贷款会影响房地产供给,因而亦会影响当年房价的波动。将两者结合起来,根据方程(1)可得:
| $ \begin{array}{l} \;\;\;\;{{\rm{P}}_{{\rm{it}}}}{\rm{ = \mathsf{ α} }}{{\rm{P}}_{{\rm{i, t - 1}}}}{\rm{ + }}{{\rm{ \mathsf{ β} }}^{\rm{'}}}_{\rm{0}}{\rm{ + }}{{\rm{ \mathsf{ β} }}^{\rm{'}}}_{{\rm{it - 1}}}{\rm{LOA}}{{\rm{N}}_{{\rm{it - 1}}}}{\rm{ + }}{{\rm{ \mathsf{ β} }}^{\rm{'}}}_{{\rm{it}}}{\rm{LOA}}{{\rm{N}}_{{\rm{it}}}}{\rm{ + }}{{\rm{ \mathsf{ λ} }}_{\rm{t}}}\\ {\rm{ + }}{{\rm{ \mathsf{ η} }}_{\rm{i}}}{\rm{ + }}{{\rm{ \mathsf{ ε} }}_{{\rm{it}}}} \end{array} $ | (8) |
其中,i=1, 2, …,31,代表 31个省份,P代表房地产价格,LOAN代表房地产开发贷款,λ、η为虚拟变量。在方程(5)、方程(7)的约束下,通过广义矩阵估计,得到如表 1所示的结果:
| 表 1 房地产价格与房地产开发贷款的GMM估计 |
表 1显示,在显著水平α=0.05下,模型整体的拟合程度较理想。Wald (joint)检验结果为“**”, 即p=0.000,表明拒绝了参数向量不相关的原假设,整个模型显著;Wald (dummy)检验结果为“**”,即p=0.000,同样拒绝了虚拟变量不相关的原假设,因而也是显著的。在对模型自相关性方面检验中,AR(1)检验结果为“*”,此时p=0.017<0.05,表明模型拒绝了不存在一阶自相关性的原假设,即模型存在一阶自相关性,但是AR(2)检验的p值为0.123,大于0.05,表明模型不存在二阶自相关性。因而,模型整体的回归拟合还是相当理想的。
可见,在显著水平α=0.05的情况下,变量P(-1)、LOAN(-1)均通过了显著性检验;变量LOAN的p值大于0.05,没能通过t检验。从这一回归结果看,房地产价格P不受当期银行信贷(LOAN)的影响,但与上一年的银行信贷规模(LOAN(-1))存在着相关性,且方向相反。这意味着,房地产价格的上涨导致了银行信贷的扩张,而不是过度的银行信贷导致了房地产价格的上涨,即房价每上涨1个百分点,将会吸引0.001 4个百分点的银行信贷资金流入房地产市场。这一结论证明了假说1。
此外,从检验结果中还可以发现一个很有意思的现象:上一年的房价对当年房价存在着很强的正相关性。从数量上看,表现为上一年房价每上涨1.108 41%,当年房价将会上涨1%。这说明,投资者会根据过去价格变化的资料和信息,在准备购房前就对当期价格作出预期,当认为未来房价不断攀升时,投资者纷纷购房置业,从而推动当期房价的上涨。
(二) 房地产开发贷款与房地产供给的GMM估计在我国,银行信贷规模取决于国家的货币政策。然而,货币政策有较强的时滞性,这是因为货币政策的传导环节多,需要通过影响利率后再影响投资和消费。根据蛛网模型,房地产市场中上一年的供给会对下一年产生影响。因此,在分析房地产开发贷款对其供给的影响时,应当将这两方面结合起来予以考虑。
根据方程(1),可得方程(9),
| $ \begin{array}{l} \;\;{{\rm{S}}_{{\rm{it}}}}{\rm{ = \mathsf{ α} }}{{\rm{S}}_{{\rm{i, t - 1}}}}{\rm{ + }}{{\rm{ \mathsf{ β} }}^{\rm{'}}}_{\rm{0}}{\rm{ + }}{{\rm{ \mathsf{ β} }}^{\rm{'}}}_{{\rm{it - 1}}}{\rm{LOA}}{{\rm{N}}_{{\rm{it - 1}}}}{\rm{ + }}{{\rm{ \mathsf{ β} }}^{\rm{'}}}_{{\rm{it}}}{\rm{LOA}}{{\rm{N}}_{{\rm{it}}}}{\rm{ + }}{{\rm{ \mathsf{ λ} }}_{\rm{t}}}\\ {\rm{ + }}{{\rm{ \mathsf{ η} }}_{\rm{i}}}{\rm{ + }}{{\rm{ \mathsf{ ε} }}_{\rm{i}}} \end{array} $ | (9) |
其中,i=1, 2, …,31,代表 31个省份,S代表房地产供给,LOAN代表房地产开发贷款,λ、η为虚拟变量。在方程(5)、方程(7)的约束下,通过广义矩阵估计,得到如表 2所示的结果:
| 表 2 房地产开发贷款与房地产供给的GMM估计 |
由表 2可知,在显著水平α=0.05下,模型整体的拟合程度较理想。Wald (joint)检验结果为“**”, 即p=0.000,表明拒绝了参数向量不相关的原假设,整个模型显著;Wald (dummy)检验结果为“**”,即p=0.000,同样拒绝了虚拟变量不相关的原假设,因而也是显著的。此外,对模型AR(1)、AR(2)检验表明,模型不存在自相关性;在变量的t检验上,变量LOAN的p值为0.541,大于0.05,没通过显著性检验,变量S(-1)和变量LOAN(-1)是显著的。
这一检验结果表明,当年的银行信贷资金对当年的房地产市场供给不产生显著影响,但对下一年的房地产市场供给将产生重要影响。因为房地产开发商开发设计、生产产品需要一定的时间周期,资金的投入使用具有一定的时滞性。从数量上看,上一年银行信贷资金每增加0.301个百分点,下一年的房地产市场供给将增加1个百分点。这充分表明,房地产市场对银行资金的依赖度是相当高的,同时也验证了假说2的正确性。
(三) 房地产需求与经济增长的GMM估计这里的基本面板模型仍然采用方程(1)的形式,以国内生产总值的增长代表经济增长(GDP)。由于经济增长受到周期惯性的影响,因此,本文吸纳自回归分布滞后模型的思想,将其滞后3期,具体方程形式如下:
| $ \begin{array}{l} \;\;\;{\rm{GD}}{{\rm{P}}_{{\rm{it}}}}{\rm{ = }}\sum\limits_{{\rm{k = 1}}}^{\rm{3}} {{{\rm{\alpha }}_{\rm{k}}}} {\rm{GD}}{{\rm{P}}_{{\rm{i}},{\rm{t - k}}}}{\rm{ + }}{{\rm{\beta }}^{\rm{'}}}_{\rm{0}}{\rm{ + }}{{\rm{\beta }}^{\rm{'}}}_{{\rm{it - 3}}}{{\rm{D}}_{{\rm{it - 3}}}}{\rm{ + }}{{\rm{\beta }}^{\rm{'}}}_{{\rm{it - 2}}}\\ {{\rm{D}}_{{\rm{it - 2}}}}{\rm{ + }}{{\rm{\beta }}^{\rm{'}}}_{{\rm{it - 1}}}{{\rm{D}}_{{\rm{it - 1}}}}{\rm{ + }}{{\rm{\beta }}^{\rm{'}}}_{{\rm{it}}}{{\rm{D}}_{{\rm{it}}}}{\rm{ + }}{{\rm{\lambda }}_{\rm{t}}}{\rm{ + }}{{\rm{\eta }}_{\rm{i}}}{\rm{ + }}{{\rm{\varepsilon }}_{{\rm{it}}}} \end{array} $ | (10) |
其中, i=1, 2, …,31,代表 31个省份,GDP代表经济增长,D代表房地产市场需求,λ、η为虚拟变量。在方程(5)、方程(7)的约束下,通过广义矩阵估计,得到如表 3所示的结果。
| 表 3 房地产需求与经济增长的GMM估计 |
由表 3可知,在显著水平α=0.05下,模型整体拟合得非常理想。Wald (joint)和Wald (dummy)检验结果均为“**”,都拒绝了原假设,因而参数向量和虚拟变量都是显著相关的。在对模型AR(1)的检验上,检验结果为“**”,即p=0.008<0.05,则表明模型存在一阶自相关性。变量的t检验结果表明,各个变量都通过了显著性检验,因而选取的变量都是有效的。
这一检验结果表明,我国的当年经济增长一方面受前几年经济增长的影响,但主要取决于上一年的经济增长;另一方面则取决于当年房地产市场的需求。从回归结果看,上一年经济增长比房地产市场需求对GDP的促进作用要强,即上一年的经济增长对当期1个百分点GDP的贡献率为0.56%,而房地产市场需求对1个百分点GDP的贡献率仅为0.16%。这也证明了假说3是正确的。但是,由此也看出,房地产市场需求对经济增长的推进作用并没有像预期的那样显著。
五 小结通过上述实证分析,本文得出的我国房地产市场波动与银行信贷、经济增长之间关系的主要结论及其启示是:
第一,就银行信贷、房地产价格的关系而言,房地产价格的持续上涨增加了银行信贷的冲动,而不是相反,即房价每上涨1个百分点,将会吸引0.001 4个百分点的银行信贷资金流入房地产市场。同时,上一年房价每上涨1.108 41%,当年房价就上涨1%。如此循环往复,必然诱导银行信贷资金源源不断地流入房地产领域,从而引发房地产市场过热。这提示我们,有关部门在对房地产市场进行调控时,其首要的任务和目标,应当是抑制房价过快上涨,这样才能有效缓解因银行信贷过于集中于房地产开发领域而导致的经济发展不平衡。
第二,就银行信贷和房地产供给的关系而言,当年的银行信贷资金对当年的房地产市场供给不产生显著影响,但对下一年的房地产市场供给将产生重要影响,即上一年银行信贷资金每增加0.301个百分点,下一年的房地产市场供给将增加1个百分点。这一方面反映了我国房地产行业对银行资金较高程度的依赖,另一方面也说明银行信贷的增加将提高市场的有效供给。因此,有关部门在对房地产市场进行调控时,一方面不应当采取过于宽松的金融政策,而应当防止信贷资金过分地流入房地产市场,以警惕金融系统风险的产生,避免资产泡沫的膨胀;另一方面,由于我国的房地产业供给约束非常严重,在居民收入增长时无法满足居民的需求(李宏瑾,2005),所以,保持适度的银行信贷流入,也是为了达到增加房地产供给、平抑房价之目的所必需的条件。
第三,就房地产市场与经济增长的关系而言,房地产市场的需求对经济增长的促进作用比我们预想的要小,当期的房地产需求对每一个百分点经济增长的贡献仅为0.16%。但是,我们并不能以此否定房地产行业对国民经济各行业的带动作用。我们更应看到房地产行业对经济增长所具有的间接促进作用,即房地产业的贡献还体现在对制造业、建筑业和相关生产性服务业的拉动上。因此,有关部门在对房地产市场调控时,一方面,应当严格打压地方政府推行“土地财政”的冲动,禁止炒地皮、拉升房价等违规行为;另一方面,考虑到从长期看,由于房地产市场需求的变动会影响经济增幅,过度收紧的宏观经济政策将影响经济的发展,所以,一旦房价企稳,对于一些临时性的过于严厉的紧缩政策应适当放松,从而确保房地产业以及整个国民经济稳定、健康发展。
段忠东、曾令华、黄泽先, 2007, 《房地产价格波动与银行信贷增长的实证研究》, 《金融论坛》第2期。 |
高波、王斌, 2008, 《中国大中城市房地产需求弹性地区差异的实证分析》, 《当代经济科学》第1期。 |
李宏瑾, 2005, 《房地产市场、银行信贷与经济增长——基于面板数据的经验研究》, 《国际金融研究》第7期。 |
李熙娟、李斌, 2006, 《房地产业与国民经济增长的实证研究》, 《商业研究》第4期。 |
彭建平、张建华, 2007, 《基于动态面板数据模型的我国R & D投入效果实证分析》, 《系统工程》第12期。 |
皮舜、武康平, 2004, 《房地产市场发展和经济增长间因果关系——对我国的实证分析》, 《产业组织研究》第3期。 |
夏丹, 2007, 《我国房地产业发展与经济增长关系的实证分析》, 《重庆工学院学报(社会科学版)》第10期。 |
邹朋飞, 2008, 《银行信贷、房地产价格与实际产出关系的经验研究》, 《山西财经大学学报》第12期。 |
Arellano, M. and Bover, O., 1995, "Another Look at the Instrumental Variable Estimation of Error Components Models", Journal of Econometrics, Vol.68. |
Arellano, M., et al, 1991, "Some Tests of Specification for Panel Data: Monte Carlo Evidence and an Application to Employment Equation", Review of Economic Studies, Vol.58. |
Blundell, R. W., et al, 1998, "Initial Conditions and Moment Restrictions in Dynamic Panel Data Models", Journal of Econometrics, Vol.87. |


