一 引言

在社会经济活动中，经济行为主体根据对价格指数变化趋势的观察和判断来形成通货膨胀预期，从而调整自身的经济行为。经济理论一般认为，完全预期到的通货膨胀一般不会扭曲资源配置和影响社会福利，因为工资、名义利率等会根据预期提前作出同步调整；但一旦经济行为主体对通货膨胀率的预测水平和实际水平不一致时，就会产生通胀预期不确定性。通胀预期不确定性通常被认为是联系通货膨胀和实际经济活动的中间环节，也即高通货膨胀产生的经济成本是由于微观经济主体对未来通货膨胀预期的不确定性增加，并据此调整自身的经济行为而引起的。由于预期的本质特征是不确定性，因此，在当前我国通胀压力逐步呈现，通胀预期有所抬头，决策层已把管理通胀预期与保增长、调结构一同纳入宏观调控范围的背景下，研究如何降低通胀预期不确定性，避免其向不利于宏观经济稳定运行的方向发展，具有重要的现实意义。

本文关注以下两个问题：第一，改革开放30多年来，在我国的经济体制改革不断深入、宏观政策频繁变化的同时，也历经多次诸如1998年亚洲金融危机、2007年美国次贷危机等的外部冲击。那么，我国的通胀预期不确定性来源主要是由于公众因经济结构、宏观经济政策变化所导致的结构型通胀预期不确定性，还是随机冲击所产生的冲击型通胀预期不确定性？对这个问题的回答，有助于揭示我国通胀预期不确定性的本质所在，同时对于货币当局有针对性地制定政策具有重要启示意义。第二，已有文献绝大多数重点关注总体通胀预期不确定性如何影响宏观经济波动，但对不同来源的通胀预期不确定性在对宏观经济波动方面的影响究竟有何差异却鲜有实证解释。对这个问题的回答，同样有助于厘清不同来源的通胀预期不确定性与宏观经济变量的相互作用机制，为货币政策合理制定提供有益启示。

现有关注我国公众通胀预期不确定性的文献并不多，结合我国经济体制改革与对外开放实践历程，从理论上分析通胀预期不确定性特点与来源分解的经验研究更是少见。本文在以下两点与现有文献有所区别：首先，就研究内容而言，国内已有研究尚未对我国通胀预期不确定性进行来源分解，因此，无法明晰究竟何种类型预期不确定性占据主导地位，这将不利于我国央行有针对性地制定货币政策。而且不同来源通胀预期不确定性对宏观经济波动的影响是否存在差异，目前还未见相关研究。其次，从研究方法看，目前国内文献测度通胀预期不确定性一般基于GARCH类模型，本文则应用具有马尔可夫机制转换异方差的时变参数模型(Time-Varying-Parameter Model with Markov-Switching Heteroskedasticity，以下简称TVP-MS模型)克服一般GARCH模型无法分解通胀预期不确定性来源的缺陷。

本文余下部分结构安排如下：第二部分对已有研究进行回顾，并提出本文的研究思路；第三部分是我国通胀预期不确定性分解的TVP-MS模型设定；第四部分是相关数据的来源与处理、TVP-MS模型估计结果及分析；第五部分考察两类不同来源的通胀预期不确定性对宏观经济的影响，并应用不可逆投资理论与不确定性关系理论对模型估计结果给出初步的解释；结论和政策启示安排在第六部分。

二 文献回顾

迄今为止，国外学者对通胀预期不确定性来源存在较多的理论分析与经验研究。理论上，Ball(1992)认为，通胀预期不确定性来源于公众无法区分类型不同的货币当局在面临通胀时采取货币政策倾向的不同。Holland(1993)加入经济参与者的预期因素, 指出在对经济结构信息不完全的情况下, 不同微观经济主体的不一致预期将导致预期不确定性的增加。Cukierman和Melzter(1986)认为，不确定性来源于机会主义货币当局的货币政策选择, 从而也可归结为货币政策体制转换的不确定性。因此，从理论上讲, 通胀预期不确定性的来源主要包括供给冲击, 货币政策体制转换的冲击和对经济结构的不完全信息等。基于上述认识，国外文献利用各种计量模型进行通胀预期不确定性的分解。例如Evans和Wachtel(1993)应用马尔可夫机制转换模型把通胀预期不确定性分解为确定性等价成分与区制不确定性成分。Davies等(2006)把通胀预测误差的方差作为通胀预期不确定性代理变量，继而将其分解为特定个体的预测误差方差和总体冲击方差。

相比国外已有的较为丰富的理论解释与实证检验，国内对通胀预期不确定性问题的研究尚不多见，为数不多的文献集中在研究通胀预期不确定性与通货膨胀水平之间的关系方面。例如赵留彦等(2005)应用马尔可夫机制转换模型将通胀预期不确定性分解为两类：未来通胀冲击的不确定性和未来通胀均值在不同区制之间转变的不确定性。苏梽芳和赵昕东(2009)从公众长期和短期预期角度，把通胀预期不确定性分解为长期通胀预期不确定性与短期通胀预期不确定性。除此之外，关于通胀预期不确定性研究的重要文献还包括全林(1996)以及周宏山、李琪(2006)等。无疑，这些文献为我们深入研究中国的通货膨胀动态过程提供了有益的启示。但是纵观国内外的研究文献，一般都采用GARCH模型来度量通胀预期不确定性，其缺憾体现在使用GARCH模型估计通胀的条件方差时，设定均值过程仅遵循单一状态，这是假定通胀预期不确定性仅仅来源于通胀冲击。而如果实际中通胀均值过程也是随时域改变的，则GARCH模型并不能充分刻画通胀预期不确定性。赵留彦等(2005)的研究虽然采用一个设定均值和条件方差均发生机制转换的模型，但其设定的均值方程的估计系数仍然为固定常数，分解得到的两类通胀预期不确定性本质上是来源于随机冲击，因此也就无法比较全面地描述其他内生冲击所带来的通胀预期不确定性。除此之外，我们还发现，不同来源的通胀预期不确定性对实际经济影响的经验研究也未见诸于国内的相关文献。其实，李拉亚(1994)早就注意到我国处于经济转轨时期特点，因而来自各方面的不确定性对通货膨胀存在着重要的影响。他指出，经济体制改革，物价改革，外汇、股票、房地产等市场以及国际市场四个方面的不确定性因素影响着经济行为主体预期的形成。李红梅(1996)则认为，通胀预期不确定性是客观的，主要受自然因素、社会因素、人为因素的影响，前两种因素可以看作是外生的，表现为经济系统所受的外部冲击，第三种因素是经济行为主体的心理预期。

上述观点对本文研究具有重要的启发作用，本文的研究思路则是在Kim(1993)研究的基础上展开。Kim(1993)应用TVP-MS模型对美国的货币增长不确定性进行了研究，把货币增长不确定性分解为两个来源，一是货币增长方程扰动项出现的异方差所引发的不确定性；二是面对货币政策的改变，经济行为主体不得不推断未知或改变的回归系数所引发的不确定性。笔者认为，通胀预期不确定性与货币增长不确定性同属于名义不确定性，因而可在同一模型框架下研究。借鉴Kim(1993)的研究思路，首先利用TVP-MS模型对通货膨胀率进行拟合，与以往自回归模型不同的是，我们设定的模型的自回归系数是随时间变化的，而随机冲击的条件方差允许在不同机制下转换。对模型估计后的通胀预期不确定性进行分解，得到两类不同来源的通胀预期不确定性，分别定义为宏观政策层面引发的预期不确定性和经济冲击引发的预期不确定性，即结构型通胀预期不确定性与冲击型通胀预期不确定性，从而对我国的通胀预期不确定性作全面的分析，继而分别考察这两类通胀预期不确定性对宏观经济的影响。

三 实证框架：TVP-MS模型 (一) 基本框架

Harrison和Stevens(1976)指出：个人对未来的不确定性不仅产生于未来随机扰动，而且也产生于对当前参数的不确定性。因此，仅把通胀预期不确定性归结于由随机冲击所引发是不全面的。本文将通胀预期不确定性的来源主要归结于两类因素，并且应用TVP-MS模型进行量化。这两类不确定性分别是：第一类是指宏观经济环境变化导致政府宏观经济政策的改变，公众对宏观经济结构认识上的变化以及政策当局相互冲突的政策目标所引发的通胀预期不确定性，此种不确定性的产生完全来自于已发生的宏观经济环境变化, 是确定性内生冲击所导致的，可定义为结构型通胀预期不确定性(structural uncertainty)。对通货膨胀率进行建模时，主要体现在通胀自回归方程中的回归系数并非固定不变，而通常采用变参数模型来描述。第二类预期不确定性则是各种未预期到的随机冲击所引发的，主要体现在通胀方程扰动项的条件方差出现异方差特征，刻画方法可以在随机扰动项中考虑GARCH效应或者具有马尔可夫机制转换效应。对于这种来源的通胀预期不确定性，称之为冲击型通胀预期不确定性。

为了把通胀预期不确定性分解为两种不同的来源，本文应用能够更好地捕捉到通胀预期不确定性机制转换的TVP-MS模型来拟合通货膨胀过程，并利用通货膨胀回归方程的预测误差的条件方差来度量通货膨胀预期不确定性。具体模型设计如下：

$ \begin{array}{l} {{\rm{ \mathsf{ π} }}_t} = {\beta _{0t}} + \sum\limits_{i = 1}^k {{{\rm{ \mathsf{ π} }}_{t - i}}} {\beta _{it}} + {\varepsilon _t}, t = 1, 2 \ldots T\\ = {X_t}{\beta _t} + {\varepsilon _t}, {\varepsilon _t} \sim N\left({0, {h_t}} \right) \end{array} $

(1)

$ {h_t} = {\eta _0}^2 + ({\eta _1}^2 - {\eta _0}^2){S_t} $

(2)

$ {\beta _t} = {\beta _{t - 1}} + {\eta _t}, {\eta _t} \sim iidN\left({0, \mathit{\Omega} } \right) $

(3)

以上各式中, X_t=(1 π_t-1 π_t-2 … π_t-k), 是1×(k+1)的解释变量的向量；β_t是(k+1)×1的时变参数的向量；h_t是ε_t的条件方差；S_t^π是取值0或者1的不可观测的两状态变量, 遵循一阶的马尔可夫过程, 决定了方差h_t所处的不同机制:当S_t=0时方差h_t=η₀²，当S_t=1时方差h_t=η₁²；p_ij则表示从状态i到状态j的转换概率:

$ \begin{array}{l} Pr\left[ {{S_t} = 1|{S_{t - 1}} = 1} \right] = {p_{11}}, {\rm{ }}Pr\left[ {{S_t} = 0|{S_{t - 1}} = 1} \right] = 1 - {p_{11}}\\ Pr\left[ {{S_t} = 0|{S_{t - 1}} = 0} \right] = {p_{00}}, {\rm{ }}Pr\left[ {{S_t} = 1|{S_{t - 1}} = 0} \right] = 1 - {p_{00}} \end{array} $

以上就是描述我国通货膨胀动态过程的TVP-MS模型。显然，上述模型已是状态空间模型的表示形式，可用Kalman滤波算法进行估计。因为本文感兴趣的只是模型预测误差的条件方差而非其余参数，因此，具体的推导过程参见Hamilton(1994)，后文我们给出一个大致的估计步骤。这里我们只给出预测误差的条件方差的估计值:

$ {{\tilde H}_t} = {{\tilde H}_{1t}} + {{\tilde H}_{2t}} $

(4)

$ {{\tilde H}_{1t}} = {X_{t - 1}}{{\tilde R}_{t/t - 1}}X{\prime _{t - 1}} $

(5)

$ {{\tilde H}_{2t}} = \sum\limits_{j = 0}^1 {Pr\left({{S_t} = j|{\psi _{t - 1}}} \right){\sigma ^2}_j = {\sigma _0}^2 + \left({{\sigma _1}^2 - {\sigma _0}^2} \right)Pr\left({{S_t} = j|{\psi _{t - 1}}} \right)} $

(6)

其中，${{\tilde H}_t}$即为总体通胀预期不确定性，而${{\tilde H}_{1t}}$为结构型通胀预期不确定性，${{\tilde H}_{2t}}$为冲击型通胀预期不确定性。

(二) 模型估计方法

TVP-MS模型主要是利用状态空间模型的Kalman滤波和Hamilton滤波来估算的, 但Kalman滤波和Hamilton滤波往往无法进行复杂的数据处理, 对此, Kim(1993)在Kalman滤波和Hamilton滤波基础上提出了一种近似算法, 很好地解决了TVP-MS模型的估算。贾俊雪等(2006)将参数估计过程概述为如下步骤:第一步是在给定参数初值的情况下, 利用Kalman滤波给出基于状态变量S_t=i和S_t=j(i, j=0, 1)与t-1期信息的条件时变参数β_t|t-1^{(i, j)}、条件转换概率Pr_t|t-1^{(i, j)}、通货膨胀率的条件预测误差ξ_t|t-1ⁱ和条件预测误差的方差H_t|t-1^{(i, j)}; 第二步是基于第一步的估算值, 利用Kim的近似滤波算法给出基于t期信息和S_t=j的时变参数β_t|t^j以及转换概率Pr_t|t^j; 第三步是以第二步的估算值作为第一步的初值继续重复第一步和第二步, 直到收敛为止, 从而得到对数似然函数, 并进而得到参数的最大似然估计; 第四步是在得到全部模型参数的估算值后, 以全部样本信息为基础进行更新, 从而给出时变参数和转换概率的平滑推断。其中对数似然函数为:$LL = \sum\limits_{t = 1}^T {{\rm{log}}\left({f\left({{\pi _t}|{\psi _{t - 1}}} \right)} \right)} $, 而$f\left({{\pi _t}|{\psi _{t - 1}}} \right)$为π_t的边际密度:

$ f\left({{\pi _t}|{\psi _{t - 1}}} \right) = \sum\limits_{i = 0}^1 {\sum\limits_{j = 0}^1 {f\left({{\pi _t}, {S_{t - 1}} = i, {S_t} = j|{\psi _{t - 1}}} \right)} } {\rm{ }} = \sum\limits_{i = 0}^1 {\sum\limits_{j = 0}^1 {} } \frac{1}{{\sqrt {2\pi H_{_t}^{(i, j)}} }}{\rm{exp}}\left\{ { - \frac{{{{\left({\xi _{t|t - 1}^i} \right)}^2}}}{{2H_t^{(i, j)}}}} \right\} $

其中，ψ_t-1为直到t-1期的所有信息集, H_t^{(i, j)}为状态变量S_t-1=i和S_t=j时预测误差ξ_t|t-1ⁱ的条件方差。需要指出的是, 条件方差度量了通胀预期不确定性, 其值越大意味着通胀预期的不确定性越大。

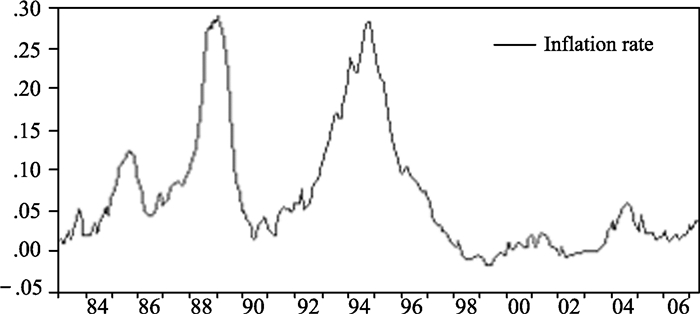
四 通货膨胀预期不确定性来源分解 (一) 样本数据说明

通货膨胀率经月度同比消费者价格指数(CPI)换算所得，样本期间为1983年1月至2007年5月。我们采用的反映宏观经济活动的指标是工业增加值率，并利用X-12进行季节调整，这是因为我国缺乏月度的GDP增长率数据，样本期间为1994年1月至2007年5月。之所以通货膨胀率和工业增加值样本期间不同，原因是我国自1994年1月才公布月度的工业增加值率数据。因此，对通胀预期不确定性进行分解研究时，考察的样本期间为1983年1月至2007年5月，而研究不同来源的通胀预期不确定性对宏观经济的影响时，考察的样本期间为1994年1月至2007年5月。以上数据来源于中经网数据库。图 1给出了我国通货膨胀率的动态路径变化。

从图 1可以发现，我国改革开放以来，经济经历数次通胀、紧缩以及两者的相互转换，通货膨胀过程在不同阶段的行为特征差别明显，其动态经历了高涨——温和膨胀——紧缩——再度温和膨胀的过程。这个复杂的变化过程意味着我国通货膨胀率变化路径中很可能出现了显著的结构性转变，因此，普通的自回归模型因为忽略我国通货膨胀特点而可能无法很好描述其数据特征，而带有马尔可夫机制转换异方差的时变参数模型应是描述和分析通货膨胀路径的动态属性更好的替代模型。关于这一点，龙如银等(2006)应用马尔可夫机制转换模型拟合中国通货膨胀动态波动的研究为本文模型设定提供了很好的实证支持。

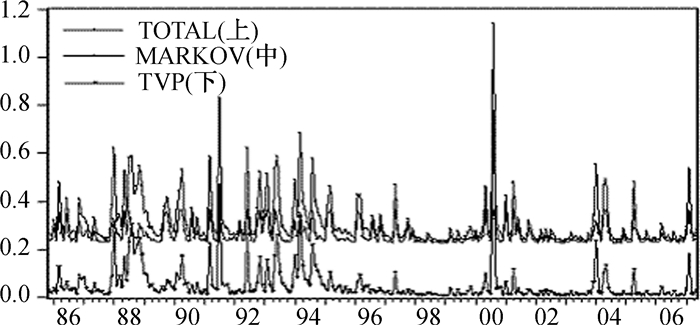
(二) TVP-MS模型估计结果及其解释

在对TVP-MS模型进行估计之前，先对通货膨胀率时间序列进行单位根检验。ADF检验结果显示，在由AIC准则确定的最优滞后阶数为15并包含截距项的条件下，ADF统计值为-2.62，而10%的临界值为-2.57，因此在10%水平下拒绝通胀过程存在一个单位根的零假设，即通胀率过程为平稳过程，由此我们可以较有把握地认定通货膨胀的数据特征是符合模型的前提条件的。TVP-MS模型估计结果如表 1所示。从表 1的参数估计结果看，大部分参数都在10%水平下具有显著性。进一步对模型估计后得到的残差及其平方序列进行自相关检验(结果见表 1下方，Q统计值括号内数值为伴随概率)，我们发现两种序列都不存在序列相关。以上检验表明，我们设定以TVP-MS模型来拟合中国的通货膨胀动态过程是必要而且合理的。图 2给出了总体通胀预期不确定性(Total)动态特征，以及分解后得到的结构型通胀预期不确定性(TVP)、冲击型通胀预期不确定性(Markov)的变化趋势。TVP-MS模型中两个重要参数p₁₁和p₀₀分别表示通胀预期不确定性在高位状态和低位状态得以维持的平滑概率，从估计系数看，总体而言，通胀预期不确定性在低位状态的持续性要大于其在高位状态的持续性，低位的平均持续期大约为4个月(1/(1-0.756)≈4)，而高位的平均持续期大约为1.9个月(1/(1-0.484)≈1.9)。这个结论基本与图 2所体现的我国通胀预期不确定性的特征相吻合。

从图 2可以看到，总体上看，上世纪整个80年代和90年代初中期集中地出现了较高的通货膨胀预期不确定性，并且处于频繁变动之中。此后也经历了几次高的预期不确定性，但很快地下降，持续的时间比较短暂。具体而言，1995年以前通货膨胀率在两种状态之间交替转换，每一种状态的持续时间都比较短。例如1988年，很难预期政府是否继续以更大的力度推进价格市场化，是否会继续过度扩张的信贷政策，否则不会导致当时大规模的银行挤提和一些城市的抢购风潮。反映在图 2上，1988年期间，通胀预期不确定性骤然升高。1992年下半年至1995年初是改革以来第二个高通胀阶段, 过度的货币供给、粮价改革以及能源价格的提高是造成本次物价上涨的直接诱导因素，再加上资本市场的过度投机，通胀预期不确定性再次达到高峰，这反映了这一阶段价格改革的“走走停停”的曲折过程以及政府宏观经济政策的频繁变动。1995年以后通货膨胀相对稳定在低预期不确定性状态，状态的转换并不频繁。1998年中央银行逐步建立以基础货币为操作目标、货币供应量为效果目标的货币政策调控机制，货币政策总体保持一种相对稳定态势，使通货膨胀保持一种低预期不确定性的稳定状态。2004年为治理经济过热，货币政策发生了明显转变，导致通胀预期不确定性出现短暂的高企。

从图 2上直接观测，我们还发现一个重要结论，即自1996年经济实现“软着陆”以后，我国通胀预期不确定性似乎发生了结构性变化。从已有理论分析来看，大部分文献支持1995—1997年是通货膨胀动态过程的结构变化点(例如：刘金全等，2006；张成思，2008)。而从现实来看，1996年经济实现“软着陆”以后，中央银行实行的以货币供应量为中介目标、货币政策透明度提高等一系列货币政策系统性改进是可以解释这种结构性变化的。以下对三种通胀预期不确定性的简单统计支持了上述判断。在整个样本期内，总体预期不确定性的均值为0.3, 但是, 从1985年至1995年, 总体预期不确定性的均值为0.34。这表明就平均意义而言，1996年之前的通胀预期不确定性要高于1995年以后的预期不确定性。而1996年之后，除了2000年1月左右通货膨胀预期不确定性较高外，其他大部分时间都处于低预期不确定性。从预期不确定性的来源角度看，冲击型通胀预期不确定性占据了主导地位，其样本均值为0.26, 解释了86%的总体预期不确定性；而结构型通胀不确定性仅仅解释了其余的14%的总体预期不确定性。但是我们也发现整个样本区间内，有几次发生结构型通胀预期不确定性高于冲击型通胀预期不确定性的情况，例如1988年10月、1991年9月以及2000年9月。上述特征与1996年之前由计划经济体制逐步过渡到市场经济体制，因经济结构变化、宏观经济政策频繁出台，以及之后我国宏观经济遭受外部冲击次数较多是分不开的：1996年以前正是我国货币政策及其调控机制和宏观经济发生相对剧烈频繁变化的时期。例如，1992年以后我国经济出现一轮快速增长并于1994年左右出现了经济过热，为了遏止高企的通胀率，政府实施了紧缩性宏观政策。1995年，我国货币政策目标发生了明显转变，从以往的“稳定货币，发展经济”的双重目标转变为“保持货币币值稳定，并以此促进经济增长”，与此同时，央行开始对货币政策调控机制进行改革，实现由直接调控向间接调控的逐步转变。正是这些宏观政策层面上的频繁变化以及宏观经济的剧烈波动，使得公众无法适应剧烈变化的宏观经济环境而导致预期不确定性上升。1996年经济成功实现“软着陆”以后, 总体通胀预期不确定性、结构型通胀预期不确定性与冲击型通胀预期不确定性均呈现逐渐下降的趋势。然而在这一时期内，冲击型通胀预期不确定性相对于结构型通胀预期不确定性始终占据主要部分，这反映了随着1994年我国市场经济体制的确立, 我国同世界经济的联系更加紧密、遭受的随机外生冲击更加显著, 且波动剧烈, 如1998年开始的东南亚金融危机、2003年的“非典”, 以及2007年世界能源与资产价格泡沫的冲击影响。而与此同时, 随着我国市场经济体制的不断完善, 我国宏观经济调控能力也不断提高, 尤其是1996年实行稳健的宏观经济政策以后，公众的结构型通胀预期不确定型始终低于冲击型通胀预期不确定性。

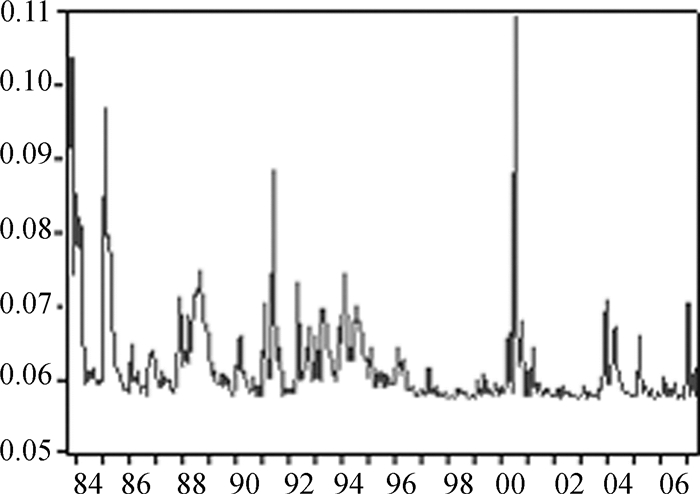
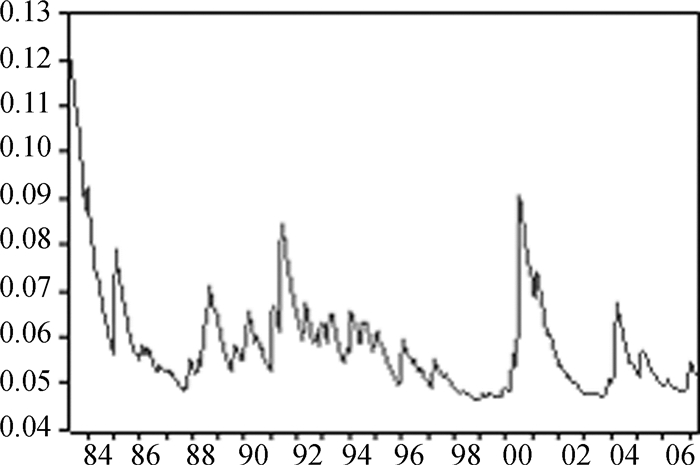
为了与其他模型度量的预期不确定性对比，本文还给出了TVP模型与GARCH模型所度量的通胀预期不确定性，分别见图 3和图 4。我们发现，两者度量的通胀预期不确定性与TVP-MS模型度量的通胀预期不确定性有着相似的动态路径。然而通过对TVP模型估计后得到的向前一步预测误差序列(已标准化)及其平方项进行自相关检验，我们发现，标准化的预测误差序列不存在序列相关，而预测误差的平方序列在10%的置信水平下存在自相关。这个发现表明，条件方差的动态过程并没有完全被TVP模型所解释。对GARCH模型估计后的预测误差进行自相关检验，我们同样发现，GARCH模型也存在类似现象。这一步证实应用TVP-MS模型拟合中国通货膨胀动态过程的合理性和正确性。

五 不同类型通货膨胀预期不确定性对宏观经济的影响

下面具体考察我国通胀预期不确定性对宏观经济稳定的影响，主要就两种不同类型的通胀预期不确定性对工业增加值率的影响作简要分析。

Kim(1993)假定实际GDP是由两个不可观测的成分构成。遵循这个思路，我们同样假定工业增加值率也是由两个不可观测成分(Unobserved Component)构成。第一个成分服从带有漂移项的随机游走过程，第二个成分则是一个自回归过程。检验不同类型通胀预期不确定性对产出增长率波动的影响的实证模型设计如下：

$ {y_t} = y_t^\tau + y_t^c $

(7)

$ {\rm{ }}y_t^\tau = y_{t - 1}^\tau + {\gamma _{{S_t}}} + {\rho _1}{H_1}t + {\rho _2}{H_{2t}} $

(8)

$ y_t^c = {\beta _1}y_{t - 1}^c + {\beta _2}y_{t - 2}^c + {\beta _3}{{\tilde \psi }_{t|t - 1}} + {\xi _t}, {\xi _t} \sim N\left({0, {\sigma ^2}} \right) $

(9)

$ {\gamma _{{S_t}}} = {\gamma _0} + {\gamma _1}S_t^y\;\;\;{S_t}^y = 0,1 $

(10)

$ Pr\left[ {S_t^y = 1|S_{t - 1}^y = 1} \right] = {q_{11}}, Pr\left[ {S_t^y = 0|S_{t - 1}^y = 1} \right] = 1 - {q_{11}} $

$ Pr\left[ {S_t^y = 0|S_{t - 1}^y = 0} \right] = {q_{00}}, Pr\left[ {S_t^y = 1|S_{t - 1}^y = 0} \right] = 1 - {q_{00}} $

其中, y_t是工业增加值率, y_t^τ和y_t^c分别是其趋势成分和周期成分, γ_St是漂移项, ${{\tilde \psi }_{t|t - 1}}$是通货膨胀率的一步向前预测误差, 反映了非预期的通货膨胀率增长。

由于产出方程中含有由前面通货膨胀方程模型所产生的解释变量H_2t和H_1t，如果应用两步法直接回归，容易导致“Pagan批评”。Pagan(1984)指出，两步法属于局部均衡方法，可能导致“生成回归量”(generated regressor)问题，从而影响到检验统计量的分布，造成统计推断无效。因此，我们利用极大似然法对通货膨胀方程和产出方程同时进行估计，可以有效地避免“Pagan批评”。联合估计最终结果列在表 2中。对表 2中三个模型估计后得到的残差进行自相关检验和ARCH效应检验。我们发现三个模型的残差及其平方序列已不存在自相关，也不存在ARCH效应。

从模型1的估计结果看, ρ₁的估计系数为负, 然而在5%水平下并不显著, 这表明由宏观政策层面引发的通胀不确定性有助于产出增长稳定, 但是这种影响并不明显; ρ₂的估计系数为正, 而且在1%水平下显著, 这意味着经济冲击引发的通胀预期不确定性对产出增长波动的影响是正向的; β₃的估计系数为正, 而且在1%水平下显著, 这表明非预期的通货膨胀冲击加剧了工业产出的波动。模型2和模型3分别在模型1基础上去掉变量H_1t和H_2t后得到, 重新进行联合估计, 我们发现，除了系数的大小有微小的变化之外, 系数的正负和显著性与模型1基本一致。

上述的发现是一个很有意思但又很重要的结果，下面我们给出一个初步的解释。经济理论一般认为通胀预期不确定性对产出增长的影响主要体现在它对投资的影响。例如，不可逆投资理论认为，在不确定性条件下，投资具有延迟性，企业可能将投资推迟，等到新信息来到时再做决策。即如果投资成本较高或者不可逆，投资者就有动机去推迟投资并等待新的信息到来以避免投资失误，由此就造成投资降低从而影响产出增长率。许多的实证检验的结论也支持了上述理论，例如Dixit和Pindyck(1994)的一项实证研究发现，通货膨胀及其波动是影响投资不确定性的重要解释变量，投资和通货膨胀率成反比关系。我们注意到，随着我国社会主义市场经济体制的建立和企业所有权结构的多元化，企业投资逐渐摆脱政府投资的特征，更多地体现了微观经济主体的动机和效果，成为一个追逐利润的能动主体，企业投资成为中国经济增长的重要因素，贡献份额呈现上升之势(马冀勋，2003)。而且，如果我们假定现实中的经济行为主体具有贝叶斯信念，并且在作决策时把通货膨胀率作为一个重要的参考因素，那么，以上实证结果可以在不可逆投资与不确定性理论的分析框架下得到解释。这个理论认为，不确定性与新信息的价值是正向关联的，在Kim(1993)的分析框架下，不同来源的不确定性对新信息价值具有不同的影响。来自于政策层面的不确定性上升，新信息的价值上升，这就给了经济行为主体激励以推迟不可逆投资，因此，政策层面的不确定性对宏观经济的影响是负面的。而对于经济冲击所引发的不确定性上升，新信息的价值却是下降的，因此，在作不可逆投资决策时，信息的价值较少。关于这一点，我们从我国企业对利率变化反应迟钝这一现象中就不难看出。

六 结论与政策启示

本文应用TVP-MS模型把通胀预期不确定性分解为结构型通胀预期不确定性与冲击型通胀预期不确定性两种来源，探讨了何种类型通胀预期不确定性是主要来源，在此基础上，检验了两种不同来源的通胀预期不确定性对宏观经济的影响，得到如下结论与启示：

第一，带有马尔可夫机制转换异方差的时变参数模型更适合拟合中国通货膨胀的动态过程，由此得到的通胀预期不确定性，比单纯的TVP和GARCH模型所度量的结果，更为全面地描述了中国的通胀预期不确定性。

第二，我国通胀预期在1996年之前出现了较高的不确定性，此后的大多数时间则处于较低的不确定性状态，而且由随机冲击引发的在总体上占据主导地位，占总体不确定性的86%；由宏观政策层面引发的结构型通胀预期不确定性虽处于从属地位，但在某些时期其相关数值超过前者。虽然目前冲击型是通胀预期不确定性的主要来源，但对于结构型通胀预期不确定性可能给经济运行带来的危害，同样不能忽视。

第三，不同类型的通胀预期不确定性对宏观经济的影响是不同的。冲击型通胀预期不确定性加剧了产出增长率的波动；而结构型通胀预期不确定性则可以减缓产出增长率的波动，但是，这种效应并不显著。

上述结论对于我国宏观政策的制定与实施具有一定的启示意义。后金融危机时代，通胀预期显现已是不争的事实。把握通胀预期不确定性来源是合理制定政策的前提，政策层应区别对待两种不同类型的通胀预期不确定性，有针对性地制定管理措施。政策层一方面应尽量保持政策的延续性、稳定性。“急刹车”或者“硬刹车”都不可取，它会导致激烈波动，误导公众，使不确定性瞬间上升。此外，有效控制通货膨胀的政策应该使通货膨胀长期可预测，因此，中央银行应加强与公众信息沟通，增强货币政策透明度，这有助于引导公众合理的通胀预期，从而降低公众的结构型通胀预期不确定性。另一方面，要充分认识我国现行经济发展方式和经济结构存在的问题，坚定不移地推进改革，以增强应对随机冲击(尤其是外部冲击)、保持物价水平基本稳定的能力，把冲击型通胀不确定性对经济的危害程度降至最低。另外，政府在宏观经济稳定政策的制定和实施时，同样需要充分考虑到不同类型的通胀预期不确定性及它们对宏观经济稳定影响的特点，从而真正给出确保经济持续稳定增长的“良方”。