“一致性”(agreement)指句法成分之间须保持性、数、格上的一致等等。部分语言所要求的主谓/谓宾一致性(agreement with subject/object)反映了句法操作的要求。

汉语在“数”在句法上没有强制要求，那么，汉语究竟有没有“数的一致性”？

汉语中一直都有语义上的单、复数之分，这一区分对不少语言现象都具有制约作用，例如，

(1) 他们都[总括]来了。

(2) *他都[总括]来了。

(3) 领导班子的成员年轻了。

(4) *他年轻了。

例句(1)、(2)、(3)和(4)合法性的对立就是汉语一致性的表现，它是语义语用的，而其中“数”的确定又是由最小量这一标准决定的。

根据陈振宇、刘承峰(2009)^①，现代汉语在语义上也必须遵守的“数的一致性假设”，即一个句子中事件论元、必有论元和可有论元之间必须保持“数”的一致，如不合乎要求，则句子不合格。

作为一条语言规律，我们要打破已有句法“数”范畴的束缚，具体地去考察实体参与事件的方式：内部方式，即实体在事件过程中是否变化和怎样变化；外部方式，即同一实体参与多个事件。并借此判断最小量及名词性成分的数值，以证明“数的一致性假设”的普遍适用性。

一 实体的数和数的一致性

由谓词及其论元构成的单句反映认知层面的事件，谓词一般是对事件基本特征的描写，而论元则是对参与该事件的实体的描写。

认知语言学把事件比喻为戏剧，实体是这场戏中的各个角色，结合配价语法理论，可以从三个方面来刻画实体在事件中的定位：

1) 句位，即每个实体所处的句法位置，如同角色在舞台上的位置，句位比较确定，每一个实体占据唯一句位。

2) 语义角色，又称为论元，即参与事件的实体的语义功能。如同戏剧中的角色，语义角色一般都是确定的，或者是施事，或者是受事等等……

3) 数量，即参与事件的实体的数量，有两个层次：

一个语义角色由一个实体担任。如例(5)中由“他”一个实体担任感事：

(5) 他见过我。

二是占据同一位置、担任同样的语义角色(论元)的实体可以有多个，我们称为“一组参与者”或“一组实体”，如例(6)中“他俩”是两个实体共同担任感事这一角色。

(6) 他俩见过我。

在论元结构研究中，与数量有关的研究视角主要有两个：

一是事件中语义角色(论元)或它们所占据的句位的数量。这也是配价语法等的研究内容^①，本文不再赘述。

二是担任同样的语义角色(论元)、占据同一句位的实体参与者的数量。这一层次是“数”范畴研究的内容。

简单地讲，假设某事件共有1、2、…m个语义角色，担任每一个角色的实体数量分别是n₁、n₂、…n_m，第一个层次考察的是m的值，而我们要考察的是这些n_i的值，以及各n_i之间的关系。

Reichenbach提出把事件作为变元(论元)应用到谓词逻辑之中^②，后来Donald Davidson戴维森分析法(Davidsonian Analysis)^③和新戴维森分析法(Neo-Davidsonian Analysis)进一步修正。根据事件语义学的分析法，例(7)可以转写为逻辑式(8)：

(7) 小王用右手从桌上拿起一支铅笔。

(8) (e)(拿起(e)∧施事(e)=小王∧受事(e)=一支铅笔∧源点(e)=桌上∧工具(e)=右手)

它是以整个事件“拿”作为一个函数，而它的论元及论元的取值范围包括{e(拿起事件本身)、施事、受事、源点、工具……}，在上述句子中，论元的值为{拿起、小王、一支铅笔、桌上、右手……}。

让我们为每一个论元赋予“数”的值，可以看到，这正是一个单数事件：只有一次拿起的行为，在这个行为中，只有一个小王在施行动作，只有一支铅笔被拿起，使用一只右手，只涉及一个处所——桌上。

与之相反，我们有(9)所表复数事件可以转写为(10)：

(9) 他们各看一本书。

(10) ((e1)(看(e1)∧施事(e1)=某人甲∧对象(e1)=书1)

∧((e2)(看(e2)∧施事(e2)=某人乙∧对象(e2)=书2)

∧((e3)(看(e3)∧施事(e3)=某人丙∧对象(e3)=书3)

……

也可以形式化为(11)：

(11)

“看”这一事件须分解为若干子事件看1、看2、看3、…，其中每一个子事件都是单数事件。“各”可以称为“一一对应标记”，因为它反映了主、宾语以及事件本身的对应关系，它要求宾语必须有数量成分，否则就不能明确表示这种关系，句子一般就不能成立，如：

(12) *他们各看《红楼梦》。——他们各看一本《红楼梦》。

据此，我们把一一对应关系修正为“数的一致性假设”：

Ⅰ必有论元在数上一般必须等于事件论元，特殊情况下可以大于事件论元。

Ⅱ必有论元之间则必须相等。

Ⅲ可有论元在数上必须大于或等于必有论元。

简言之，一旦事件为复数，则其论元便都是复数，一旦必有论元为复数，则其可有论元都是复数。

必有论元一般在数上都等于事件论元，大于主要是多个事件共享一组实体的情况：

(13) 这两个孩子，不是才来北京，就是马上要离开北京。

例(13)有可能是指一个孩子才来北京，另一个马上要离开北京，这两个事件都是单数，但孩子则有两个，他们各自参与了一个事件，所以事件为单数，而必有论元为复数。

另一方面，可有论元在数上大于必有论元的情况比较常见，如：

(14) 他用两只手抓住铅笔。

事件论元和必有论元都是单数，但工具“两只手”是复数。从认知上讲，可有论元表示事件的背景，背景当然可以比前景大，不一定要和必有论元一致，但背景不能比前景小，否则会出现“浴缸里装大象”的现象，所以可有论元又受到必有论元的制约。

二 单/复数的确定参照点——“最小量”

从理论上看，“数的一致性假设”非常“理想”，如果它是普遍适用的，那么对事件语义学来说，就是一条很好的运算规律，相对于形式语义学的某些研究采用的集合论(参见Huang Shi-Zhe1996、袁毓林2005、张莉莉2001、李晓光2002)^①，“数的一致性假设”更具普遍性。

但是，有人可以举出大量的“反例”，其中“数的一致性”似乎未被满足，而句子却是成立的。如：

(15) 他们都看这本书。

(16) 许多菌子长在那块木板上。

按一般的理解，例(15)中感事“他们”是复数，而对象“这本书”是单数，好像违反了“必有论元之间数必须相等”。例(16)中施事“许多菌子”是复数，而处所“那块木板”是单数，这个例子似乎违反了“可有论元在数上必须大于或等于必有论元”。

我们认为，这两个例子实际上并非“反例”，它们都合乎“数的一致性假设”，并反证后者的普遍性。

“数”的内在机制是测量，至少包括四种：以实体为单位进行测量、以“个体”为单位进行测量、以同质性为据的测量、以事件的最小量为单位进行测量^②。前两者稳定，固化为词汇语法中的“数”，Matthews, P. H.指出，单数指实体是单一个体，而复数指实体有多个个体。^③

但是，“个体”定义并非是单复数界定的唯一理据，例(15)—(16)中，决定单复数的，是以事件的最小量为单位进行的测量。

“最小量假设”：事件要求参与事件的实体至少应该拥有的量，称为“最小量”。如果该实体实际参与的量大于最小量，则该实体在该事件中为复数；反之，则为单数。

在例(15)中，“这本书”是事件“看”的对象，句子是完成体，关注的是看的内容。一般来说，在“看”的每一瞬间最小量为极小量，“这本书”的量大于它，所以“这本书”是复数，它满足总括“都”的要求。

在例(16)中，一个菌子生长的处所即事件[生长]所要求的最小量为木板极小的一个部分，“那块木板”的总量大于它，所以是复数，它与主语“许多菌子”之间具有数的一致性。

三 “最小量”的形式化Ⅰ：实体参与事件的内部方式

在上文，我们提出了“最小量假设”，但除了例(15)—(16)，还包括前面的例(6)好像也不合乎“数的一致性假设”，下面，我们将从事件类型入手，进一步考察其对最小量确定的影响。

3.1 实体参与事件的内部方式

一个单一的事件，从其内部来看，可以区分为三大维度：

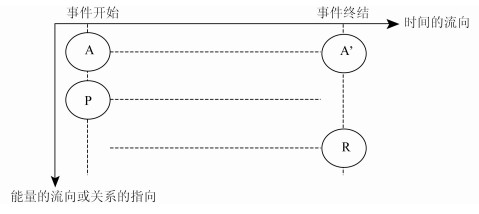
第一个维度(图中横轴)是事件在时间进程中展开的方式，包括事件的开始、延续与终结等等。

第二个维度(图中纵轴)则是在同一时间点上，事件诸元素的构造，包括事件有哪些参与者，它们之间有怎样的关系等等。

第三个维度，即纵轴与横轴交织在一起所表达的“变化”(changing)：参与者(实体)在事件的时间进程中发生着怎样的变化。

决定最小量的是第三个维度“变化”，由此形成了实体参与事件的三种内部方式：

3.1.1 整体性投入

从事件开始起，该实体就作为一个整体全部参与事件之中，而不是其部分分别参与事件；其次，该实体在事件发生的整个过程中，没有变化。

有的事件在发生过程中其论元根本就没有什么变化，或者即使有变化，这一变化也不足已在事件判断中产生参照性作用，这种事件称为静态事件，它们或者表示判断，或者表示性质状态，或者表示评价，如，

(17) 他是我哥哥。

(18) 太阳比地球大得多。

参与静态事件中的实体是整体性投入事件。当然，“太阳、地球”在历史的长河中肯定会发生某种变化，但是这种变化在认知中可以忽略，所以它是静态的。

有的事件是动态事件，但并非所有论元都会发生变化，其中某些论元也是整体性投入，所有伴随性事物，如工具、方式、目的等都是如此，一般来讲，施事也有这样的特点。如,

(19) 他看(了)一本书。

(20) 这把刀切肉不好用，要好好磨磨了。

例句(19)中的“他”参与动态事件“看”，并且在事件中的任意两个时点，“他”还是“他”，沒有什么变化。例句(20)中的“这把刀”是工具性参与成分，在“切肉”的过程中，“这把刀”保持不变。

另外，这里的“整体”指的是事件的语义内容所表示的量的全部。如，

(21) 左半边墙上有一个红色的十字。

我们所谈的是“左半边墙”，那么这里的“整体”就只是指“左半边墙”，不能理解为墙是整体而左半边墙是其中的一部分。

3.1.2 整体性变化

即实体在事件的某一阶段发生质变，而且一旦变化，涉及的就是实体的整体。分为两种情况：

一是该变化在事件的开始阶段发生，然后保持到事件终结，换言之，该实体所有的量都是在开始这一时点就全部发生了变化，如：

(22) 那盏灯亮了。

一般来说，一盏灯整体一下就全部“亮”了，然后保持到“亮”这一事件的终结。

二是变化在终结阶段才发生，终结之后保持变化后的状态，而终结之前仅仅是该变化“量”的“酝酿”阶段，如：

(23) 做椅子。

(24) 他的大脑受到了损伤，渐渐会把你忘记的。

“椅子”，在做成之前，只有木头、椅子腿、椅子面等等，只在最后组装完毕，才可以称为椅子。“忘记”也是如此，都是在终结阶段发生变化，之后一直保持“忘记”的状态。

3.1.3 阶段性变化

实体的变化是在事件过程(延续阶段)中逐渐发生并积累起来的，先是实体的一部分发生变化，然后是另一部分，最终达到事件的语义内容所表示的量。如：

(25) 他把这只鸡都吃了。

“这只鸡”是被一部分一部分地吃掉的。

根据上文分析，从“量”的角度，整体性投入、整体性变化和阶段性变化可以概化为：

整体性投入：在实体参与事件的时间进程中，任两个时点，实体参与事件的量都相等。

整体性变化：在实体参与事件的时间进程中，存在一个时点，在这一时点的前后，实体在整体上发生了质变。

阶段性变化：在实体参与事件的时间进程中，任给两个时点，实体参与事件的量都不相等，后者大于前者。

3.2 事件类型

从内部视角看，根据实体参与事件的方式的不同，单一事件可以分为两种：

3.2.1 整体性事件

当参与该事件的实体都是整体性投入或整体性变化的时，称为“整体性事件”，这时，事件不能做任何同质性的分割。例如上文例(17)和(18)。上述例句所表事件的开始和终结都不为说话者所关注，只有一种性状或评价呈现在当下，所以无法从时间上分割它。

从定义中可以看出，整体性事件对其每一个语义角色要求的最小量，是由事件的语义内容决定的，如：

(26) 他俩相互学习。

(27) 他的脸红了。

例(26)至少两个个体才能相互学习，所以“他俩”是单数；而例(27)变红的可以是极小的一块，所以“他的脸”是复数，可以看成“他的脸的甲部分红了、他的脸的乙部分红了…”诸单数事件的集合。

3.2.2 阶段性事件

当参与该事件的实体中存在阶段性变化的实体时，称为“阶段性事件”，在阶段性事件的每一个片断中，该实体都处于同样的变化之中，都是同质的，因此，整个事件可以视为一系列同质的子事件的重复。

(28) 他把这本书都看完了。

从定义可以看出，阶段性变化的语义角色在阶段性事件中的量，包括了两个方面：

一是每一个时间片断中的同质性的子事件的量，如每一眼看所阅读的内容的量。

二是整个事件最终实现的变化总量，如“一本书”。

我们认为，此时，事件对该语义角色要求的最小量是且只能是每个子事件要求的量，换言之，最小量很小很小，这必然得出结论：阶段性变化的语义角色是且只能是修辞的复数，而不管它最终实现的变化总量是多少，也不管用个体或其体实体单位测量它的数是多少，阶段性事件因此也必然是复数事件，所以例(28)可被“都”限定。

四 “最小量”的形式化Ⅱ：实体参与事件的外部方式

仅仅考虑内部方式是不够的，内部方式讨论的都是实体参与某一事件的问题，而外部方式，则考虑一个实体参与多个事件的问题。为了说明这个观点，我们首先把实体参与事件的外部方式区分为下面几种情况：

4.1 实体不变化，同时参与多个事件 4.1.1 同一实体同时参与多个同类事件

(29) 大家正在看这部电影。

(30) 他们都在猜那个问题的答案。

“这部电影”同时参与一系列“看”的子事件，“甲正在看这部电影、乙正在看这部电影…”；“那个问题的答案”也同时参与一系列“猜”的子事件，“甲在猜那个问题的答案、乙在猜那个问题的答案…”。

4.1.2 同一实体同时参与多个同类事件，同一实体同时参与多个不同的事件

(31) 他边唱边跳。

(32) 他不但长得高，而且很有力气。

我们把实体参与多个事件的能力，称为该实体的功能。在某一时点时，一个事件对实体参与能力的基本要求称为“同时的最小功能量”。一个实体若能同时参与两个或多个事件，说明每一事件只涉及该实体的部分功能，而该实体的总功能量大于单一事件所要求的最小功能量，故该实体在同时功能上是复数。反之，如一个实体在特定时点只能参与一个事件，则说明该事件“占据”了该实体的全部功能，该实体在同时功能上是单数。

4.2 实体不变化，在不同时间参与多个事件 4.2.1 同一实体同时参与多个同类事件，同一实体在不同时间参与多个同类事件

(33) 他一个劲地跳。

(34) 他看着报纸。

例(33)是瞬间事件的反复进行。例(34)中的“看”是复数事件，它由若干在时间中延续的事件片断“看1、看2、…”构成，而施事“他”在事件中不变，并在不同的时间逐一参与这些事件片断。

4.2.2 同一实体在不同时间参与多个不同的事件

(35) 他不是站岗巡逻，就是在家看书。

(36) 他除了上课，就是去图书馆自习。

“站岗巡逻”和“在家看书”、“上课”和“去图书馆自习”不能同时进行，“他”在不同时间做这些事。

一个实体在不同时间参与多个事件，首先，每个事件的时间量必须比该实体存在的时间和句中关注的时间背景要短(有关时间量问题我们将另文阐释)，除此之外，还有一个重要条件：事件之间不能相互妨碍。

如果该实体在先前事件中相互妨碍而导致消失/转化的话，就不能参与多个事件。如果它不消失/转化，那还要看它在事件中所发生的变化，是否可以恢复，如果能够复原，那么与其它事件便不冲突。如果变化不能复原，那还得再考察这一变化是否妨碍另一特定事件。

满足这一条件，称为异时的功能复数；反之，则为异时的功能单数。

五 本文的“数”系统

将上文实体参与事件的内、外方式接合在一起，我们可以得到下列数系统：

实体参与事件方式		最小量	语用的“数”
内部方式	实体整体性参与事件	由语义内容规定	整量物质单数	整量物质复数
	实体阶段性参与事件	极小	*	逐量物质复数
外部方式	实体同时参与多个事件	单一事件的功能要求	*	同时功能复数
	实体不能同时参与多个事件	单一事件的功能要求	同时功能单数	*
	实体在不同时间参与多个事件	单一事件的功能要求	*	异时功能复数
	实体不能在不同时间参与多个事件	单一事件的功能要求	异时功能单数	*
注:表中“物质单/复数”相当于陈振宇、刘承峰(2006)和刘承峰(2007)所说的“空间分割”，“同时功能单/复数”相当于该文所说的“功能分割”，“异时功能单/复数”相当于该文所说的“时间分割”①。

“数的一致性假设”，是将内部方式和外部方式合在一起考虑的，到此要补充以下两点：

Ⅳ任何一个事件及其语义角色都必须满足数的一致性假设，但是实体可以采用内、外方式中的任何一种。

Ⅴ不论一个必要论元在哪个方式是复数，其它所有语义角色便都是复数；只有当语义角色在所有方式上都是单数时，事件论元才是单数。

让我们再考察所谓“例外”的例句，可以看出，它们其实都不是例外。如上文提到的例句(6)。

(6) 他俩(整量物质复数)见过我(同时/异时功能复数)

在“x见(过)y”中，或者见过，或者没有见过，是整体性变化，又x、y至少需一个个体，所以“他俩”是整量物质复数，而“我”是整量物质单数，但是“他俩”既然是复数，事件就必然是“甲见过我”和“乙见过我”的集合，“我”同时或在不同的时间参与这两个单数的子事件，故“我”又是同时/异时功能复数。例(6)满足数的一致性假设。

(15) 他们(整量物质复数)都看这本书(整量物质/同时功能/异时功能复数)

同上。这里有歧义，如果“这本书”指同一名称的很多本书，那么他们可以同时看它；如果特指某一本书，一般情况下，在同一时间一个人看一本，那就只能是异时功能复数，当然，如果是几个人挤在一起看，那又可以是同时功能复数。

(37) 他(同时/异时功能复数)拿起两枝铅笔(整量物质复数)

与前几例相反，在“x拿起y”(整体性变化)中，x、y至少需一个一体，所以“他”是整量物质单数，而“两枝铅笔”是整量物质复数，但是“两枝铅笔”既然是复数，事件就必然是“他拿起铅笔甲”和“他拿起铅笔乙”的集合，“他”同时或在不同的时间参与这两个单数的子事件，故“他”又是同时/异时功能复数，满足数的一致性假设。

(38) 他(同时功能复数)脚踏两朵莲花(整量物质复数)

同上，只不过这是同一时间的行为，且是整体性投入。

对于相关问题的研究，陈振宇(2008)^②也进行过论述，此外，有关时间、程度等语义维度在“数”范畴中的作用，我们将另文论述。