中国目前人口老龄化年均增长率高达3.28%,约为总人口增长速度的5倍;预计2020年老年人口将达到2.48亿,占总人口的17.17%;到2050年,老年人口总量将超过4亿,老龄化水平达到30%以上(李本公,2006)。目前对老龄化问题的研究多偏重于从人口学、社会学、老年学等角度来考察,也有一些论文运用传统的空间统计模型对其区域分布进行分析。本文在空间自相关模型的基础上,构造扩展的经济自相关模型,对中国的省际老龄化分布特征进行详细阐述。
一 文献综述在早期的老龄化研究中,往往通过对指标和数据的分析描述老龄化的现状及其区域差异。刘爽(1997)根据我国各省份历次人口普查65岁及以上老年人口比例的有关数据分析得出,我国老年人口比例不仅区域差异明显,而且这种差距不断扩大并表现出某种分化离散的特点。我国各地区不同的人口老龄化程度与速度,不仅带来人口年龄结构类型在空间分布上的多样性,而且导致人口老龄化过程和老年人口问题在时间上的差异性。邬沧萍等(2004)用指标、图表分析得出我国老龄化的特点是未富先老、地区差异大。
近年来学者多运用统计和计量模型来研究人口老龄化的空间分布特征。陈茗(2001)通过对中国和日本代表性城市地区(上海、大阪)以及代表性农村地区(甘肃、岛根)的老龄化率(老年人口增长率与总人口增长率之比)比较,发现中日两国老年人口的空间分布都存在巨大的区域差异,但性质截然不同,并对其中的原因进行了归纳。袁俊等(2007)从时空角度描述了中国农村人口老龄化的分异特征,揭示了农村人口老龄化程度区域差异扩大的内在机制,并运用主成分、影响因子(经济发展、文化教育、人口自身因素)分析等方法得出,农村经济发展水平、劳动力文化教育程度的差异是影响人口老龄化程度的主要因素。林琳和马飞(2007)利用GIS空间自相关模型进行的分析发现,广州市人口老龄化的空间分布不均衡,人口迁移是人口老龄化空间差异的主要原因,人口自然增长,老年人特殊的心理、生理需求,与老年人生活密切相关的公共服务设施、养老设施等也在一定程度上影响了广州人口老龄化的空间分布。赵儒煜等(2012)利用空间回归模型估计、检验,得出区域间人口老龄化的溢出作用非常显著,周边地区通过老龄化的空间溢出效应对中心地区人口老龄化水平发挥反向调节作用的结论。查奇芬和谢明柱(2013)在对农村人口老龄化空间分布进行自相关分析的基础上,运用空间计量模型分析了经济、医疗卫生、教育、计划生育政策及人口机械迁移等因素对农村人口老龄化的影响,发现农村人口老龄化在地理上存在显著的集聚效应,并且整体上存在正的空间相关性。王泽宇等(2013)采用多项指标对人口老龄化水平进行综合测度,用空间自相关分析研究人口老龄化水平的空间关联规律,其结果表明,自1997年以来我国老龄化水平逐年升高,各省份差异明显,且差异逐渐增大;人口老龄化水平的全局空间依赖性不高,但局部空间集聚规律却很明显。
老龄化与经济发展之间关系的研究也较多。如胡鞍钢等(2012)利用包含人力资本的柯布—道格拉斯生产函数,从索洛增长理论入手,根据人口老龄化和人口增长影响经济增长的模型,实证分析了人口老龄化和人口增长率对经济增长的影响。包玉香(2012)基于新古典经济增长模型,尝试引入人口老龄化因素从而对该模型进行扩展,进一步验证了人口老龄化对区域经济发展的双重效应的存在,并认为人口老龄化程度越高,对区域经济发展影响的效应就越大,对区域经济发展的减速效应也就越明显。
总之,2000年以来我国老龄化的相关研究主要集中在老龄化与生育政策的关系、老龄化的社会经济影响、养老保障与养老保险、农村人口老龄化及养老、特殊老年群体养老、积极应对老龄化等领域(张晓青,2009)。传统空间统计模型在老龄化研究方面有一定的应用,但仅限于用地理坐标构建空间权重矩阵。本文将进一步运用经济坐标来构造经济自相关模型,研究人口老龄化与经济发展水平之间的关系。
二 中国人口老龄化现状全国31个省份(不包括港、澳、台地区)2011年的人口老龄化主要衡量指标的描述性统计如表 1所示。可见,无论是老少比、老年人口比例,还是老年人口抚养比,都显示我国进入了老龄型社会。如2011年老少比平均值为56.81%,已经严重超过联合国确定的老年型人口年龄结构国家的标准(大于等于30%)。老少比的标准差为0.219 6,说明各省份的老龄化程度差异较大。本文接下来的分析主要基于老少比这一指标,防止由于劳动力人口流动影响常住人口,从而干扰老龄化程度的度量。
| 表 1 2011年中国各省份老龄化指标的描述性统计 |
分省份来看,我国老少比从最低的西藏(20.90%)到最高的北京(100.73%)不等,但只有西藏、青海、宁夏三个省份的老少比是低于30%的。从这个角度看,我国绝大多数省份已达到国际的老龄化标准,同时全距很大,为79.83%,说明我国老少比的数值跨度比较大,人口分布不均匀,也反映出我国各省份之间的老龄化状况存在差异。老少比非常大的省份有:北京(100.73%)、上海(95.01%)、辽宁(94.83%)、天津(91.73%),这些省份除了辽宁外均为直辖市,尤其是全国政治中心北京以及商业中心上海的老少比非常大。无论是从各地区城镇居民家庭年人均可支配收入还是各地区农村居民家庭年人均纯收入来看,北京、天津和上海都远大于全国平均水平,这从一定程度上反映了老龄化程度和经济发展程度呈正相关。老少比相对较大的省份有江苏(83.29%)、重庆(77.41%)、四川(74.29%)、湖北(70.68%),大多是经济相对发达的地区。从数据可以直观看出,老少比偏低的几个省份分别为海南(34.56%)、西藏(20.90%)、青海(28.86%)、宁夏(26.16%)、新疆(33.13%),通过对比不难发现,西藏、宁夏、新疆等地老少比、老年人口比例以及老年人口抚养比都处于较低水平,这主要是由于在各省份人口死亡率相差不大的情况下,上述省份始终保持了较高的人口出生率。在2010年公布的各省份人口自然增长率中,西藏、宁夏、新疆分别以10.25‰、9.04‰和10.56‰居于前三位,这也从另一个角度解释了以上省份老少比偏低的原因。同时,在这些省份中,老、少、边、穷地区所占比例很大,由于气候不适以及经济不发达导致的医疗不完善等原因,65岁以上老年人口数相对较少,直接导致了其老少比数值很小。
三 老龄化趋势与经济发展趋势分析根据第四、五、六次全国人口普查数据,观察各省份人口老龄化的发展变化趋势,整体上看,各省份的老少比大多呈现上升趋势,但人口老龄化的速度快慢不一。
具体到老少比这一指标,其平均增长率1990—2000年为55.31%,2000—2010年为82.53%。北京、上海、江苏、安徽、湖北等16个省份的老少比增长率都曾超过80%;而河南、广东、贵州、云南、西藏、青海、宁夏、新疆这些省份的老少比偏低,但其增长率差异较大,如西藏以10.86%(1990—2000年)和44.89%(2000—2010年)的增长率处于全国最低,而贵州、青海和新疆在2000—2010年的增长率分别为77.71%、85.33%和79.61%,大致与全国平均增长率持平。
由图 1至图 4,我国各省份人口老龄化程度都呈增强趋势。按照增长率大致可分为“先慢后快”和“先快后慢”两种情形。其中“先慢后快”型的省份很多,典型的如湖北省,其人口老龄化发展速度在初期比较缓慢,1990—2000年老少比增长率仅为42.77%,低于全国平均水平12.54个百分点,而2000—2010年老少比增长率却达到了136.85%,高于全国平均水平54.32个百分点。“先快后慢”的代表则有上海市、北京市、浙江省等。以上海市为例,1990—2000年老少比增长率为83.85%,超过全国平均水平28.54个百分点,而2000—2010年老少比增长率却大幅跌至24.02%,低于全国平均水平58.51个百分点。
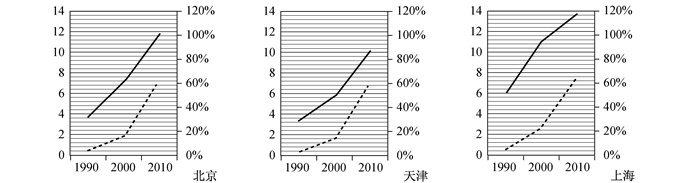
|
图 1 A类省份的老龄化趋势与经济发展趋势 |
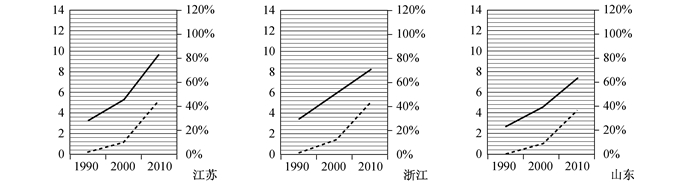
|
图 2 B类省份的老龄化趋势与经济发展趋势 |
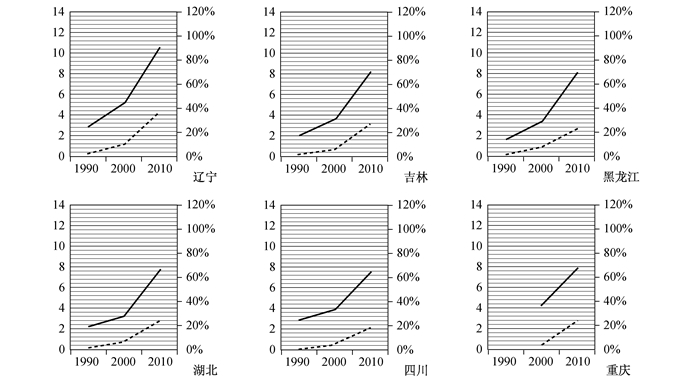
|
图 3 C类省份的老龄化趋势与经济发展趋势 |
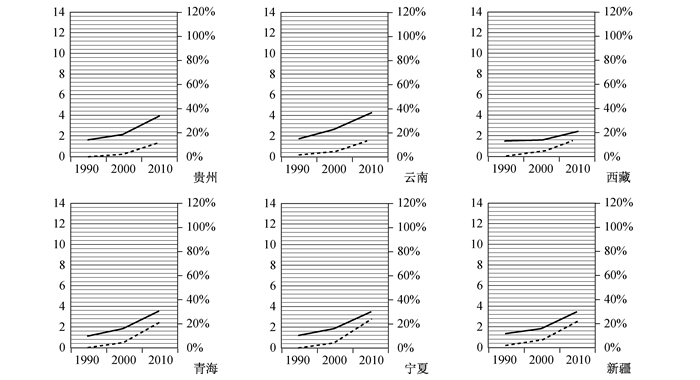
|
图 4 D类省份的老龄化趋势与经济发展趋势 |
老龄化程度与经济发展水平的关系主要表现为两种形式:一是老龄化程度与经济发展水平相当;二是老龄化程度快于经济发展水平,呈现“未富先老”的特点。接下来对一些有代表性的省份进行分类,并分别探讨老龄化发展趋势与经济发展趋势是否相符。
A类省份:北京、天津、上海。其老龄化程度和经济发展趋势如图 1,实线为老少比(单位:%),反映老龄化程度;虚线为人均GDP(单位:万元),反映经济发展情况,以下同。北京、天津、上海均为直辖市,这一属性对老龄化有一定的影响。由图 1,这三个直辖市的老少比都偏高且增长较快,2010年老少比都超过80%,上海甚至高达117.33%。从经济发展的趋势来看,这三个城市在1990—2010年经济都发生了巨大的飞跃,2010年人均国内生产总值都超过了7万元。并且老少比的变化趋势和人均GDP的变化趋势大致吻合,尤其是2000—2010年期间,两条曲线几近平行,老龄化程度与经济发展水平相当。
B类省份:江苏、浙江、山东。B类省份的老龄化现象也比较严重,2010年老少比都超过60%,江苏省甚至达到83.75%,且老少比的增长率也非常高,老龄化速度较快。由图 2,浙江省近二十年老少比这一指标几乎保持同样的速度在增长。从经济发展水平来看,江、浙、鲁三省的经济发展水平也较高,2010年人均国内生产总值都超过了4万元,居全国前列,且三省的经济发展趋势极为相近,均为“先慢后快”型。从老龄化与经济发展的关系来看,三省的老少比与人均GDP的变化趋势大致同步,老龄化程度与经济发展水平基本相当。
C类省份:辽宁、吉林、黑龙江、湖北、四川、重庆。首先,东北三省的变化趋势比较类似,大体均为“先慢后快”型。其中,吉林和黑龙江的老少比在2010年都超过了60%,而辽宁则超过了80%,老龄化情况也极为严重。且从老龄化趋势来看,东北三省人口老龄化的速度都较快。从经济发展水平看,东北三省作为中国重要的老工业基地,曾经拥有雄厚的工业基础和相对发达的城镇化水平,但是改革开放以来,由于计划经济时期逐渐形成的经济体制、产业结构和思维方式等已经不能适应市场经济的新情况,东北三省的经济发展较为落后,人均国内生产总值水平偏低。因此,该地区人口老龄化明显超前于经济发展水平,具有“未富先老”的特征。其次,湖北、四川、重庆三省份的老少比均处于中上等水平,老龄化比较严重。其中湖北和四川的老龄化发展趋势比较相近,均为典型的“先慢后快”型。重庆市比较特殊,1997年3月被确立为直辖市,1990年重庆市的人口与经济都是被统计入四川省的,因此图 3中是从2000年开始绘制。虽然曲线较短,但仍能清楚地看到重庆市十年间的情况。不同于其他三个直辖市,2010年重庆市的老少比为68.07%,而人均国内生产总值仅为2.76万元。但从发展趋势上来看,2000—2010年重庆市老龄化发展速度较快,老少比增长率达到88.96%,同时经济发展水平也有较大的增幅。需要指出的是,2010—2011年虽然只有一年,但是与其他三个直辖市不同,重庆这一年间老少比有很明显的增幅。此外,三省份的经济发展水平都较低,呈现“未富先老”的特点。
D类省份:贵州、云南、西藏、青海、宁夏、新疆。这几个省份的老少比处于较低水平,老龄化趋势及经济发展趋势如图 4所示。从图 4可直观看出其增长在1990—2000年和2000—2010年两个十年内的变化均为“先慢后快”型。而且,在1990—2000年期间除青海外,其余省份老少比的增长率均低于全国平均水平;在2000—2010年期间除青海和宁夏外,其余省份老少比的增长率均低于全国平均水平。这些省份多为少数民族聚居地,生育政策较宽,出生率较高,其中新疆和西藏的出生率分别为15.99‰和15.80‰,大大高于上海(7.05‰)、北京(7.48‰)等地的出生率,直接导致了其0—14岁的人口增多。以西藏为例,2011年西藏全区总人口为303万人,人口出生率为15.39‰,死亡率为5.13‰,自然增长率为10.26‰;人口密度为每平方公里2.21人,人口分布很不均衡,多数人口集中在南部和东部。由于耕地有限与气候高寒,以农业为主,经济较为落后。除此之外,高寒、缺氧、多山、强紫外线的高原环境对人体健康和卫生事业发展有较大影响。宁夏长年干旱,多发各种自然灾害,水土流失加剧,很多地方不适宜人类生存。贵州地理状况也不容乐观,气候不稳定,灾害性天气种类较多,对农业生产危害严重。总之,概括地说,西藏、新疆、贵州、青海、云南、宁夏这些少数民族聚居地大多以农业及畜牧业为主,地理依赖性较强,而所处地理环境较差,从而导致经济增长缓慢;另一方面,由于少数民族特殊的人口生育政策,这些地区的出生率较高,因此老龄化程度较低。
本文接下来用空间自相关模型和新构的经济自相关模型,对老龄化的省际差异和分布特征进行实证分析。
四 空间统计理论模型 (一) 空间自相关模型空间自相关反映了一个区域与其邻近区域在某一属性值上的相关程度。进行全局和局部空间自相关分析时,首先要构造空间权重矩阵,并通常依据简单邻接标准或距离标准来确定各区域是否相邻。在一阶二元邻接矩阵中,简单邻接标准是当区域i和j相邻时,空间权重矩阵的元素wij取值为1,否则为0;距离标准是指区域i和j质心间的距离在某一给定值d内时,wij取值为1,否则为0。
1.全局空间自相关性。即空间位置邻近的区域单元间观测值的相似程度,通常用Moran′s I指数和Geary′s C指数来衡量。由于Moran′s I不易受偏离正态分布的影响,故常被采用,其计算公式如下:
| $ Moran\prime s\;I = \frac{{\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {{w_{ij}}({x_i} - \bar x)({x_j} - \bar x)} } }}{{{w_0}{s^2}}} $ | (1) |
式中,xi和xj分别表示区域i和区域j的观测值,x是n个区域观测值的平均值,wij是二元空间权重矩阵的元素。
| $ Z = \frac{{I - E\left(I \right)}}{{\sqrt {Var\left(I \right)} }} $ | (2) |
式中,
2.局部空间自相关性。全局自相关分析使用一个指标来反映全局的空间自相关程度,仅能探测整个研究区域的整体分布模式,有时会掩盖局部区域的分布特征,因此有必要进行局部自相关分析,常用局部Moran指数、局部G系数和Moran散点图来衡量。
(1) 局部Moran指数。其计算公式如下:
| $ {I_i} = \sum\limits_{j = 1}^n {{w_{ij}}} ({x_i} - \bar x)({x_j} - \bar x) $ | (3) |
对局部Moran指数仍采用Zi统计量进行检验,原假设为区域i的观测值与相邻区域(通常在i的d范围内)上的观测值不相关。
| $ {Z_i} = \frac{{{I_i} - E({I_i})}}{{\sqrt {Var({I_i})} }} $ | (4) |
(2) 局部G系数。相比局部Moran指数而言,其优点在于可以确定观测值在局部的空间分布模式。例如,一个显著为正的局部Moran指数只能表明是高高聚集或者低低聚集,但结合局部G系数分析便可确定究竟是高高聚集还是低低聚集。局部G系数的计算公式如下:
| $ {G_i} = \frac{{\sum\limits_{j \ne i}^n {{w_{ij}}{x_j}} }}{{\sum\limits_{j \ne i}^n {{x_j}} }};\;{Z_{{G_i}}} = \frac{{{G_i} - E({G_i})}}{{\sqrt {Var({G_i})} }} $ | (5) |
由于无论d的大小如何,Gi都不能保持正态性,故一般不对ZGi进行检验,而是将局部ZGi和显著的局部Moran指数相结合,来判断出区域i周围的空间分布模式。
(3) Moran散点图。Moran散点图的纵轴Wz为标准化的空间权重矩阵,横轴Z为区域观测值与全局观测值均值的偏差组成的向量。其四个象限分别表示了该区域与其相邻区域的局部空间自相关性:第一象限表示高观测值区域的周围也是高值区域,即“高—高”模式;第二象限表示低观测值区域的周围是高值区域,即“低—高”模式;第三象限为“低—低”模式;第四象限为“高—低”模式。通过Moran散点图可识别全局空间中主要存在哪几种分布类型。
(二) 经济自相关模型在传统的空间自相关模型中,空间权重矩阵元素的值是根据各区域地理位置是否相邻来确定的。这意味着传统的空间权重矩阵仅反映了地理位置信息, 以采用距离标准构建权重矩阵的情形进行说明,在传统模型中,通常根据区域质心的经纬度来确定各区域的位置坐标(本文称之为地理坐标),然后再根据地理坐标点间的距离来确定权重矩阵中对应的元素值。
本文主要研究观测值对各区域经济发展水平的依赖性,因此用经济坐标替代地理坐标,构造经济自相关模型,选取GDP和CPI这两个能够刻画区域经济发展水平的指标,作为该区域的坐标值(本文称之为经济坐标),再根据欧式距离标准来确定其在空间矩阵中对应的元素值。用地理坐标构建的空间权重矩阵反映的是区域单元空间位置的相邻性,而使用经济坐标构建的权重矩阵则反映了区域单元经济发展水平的相近性。将基于经济坐标构建的权重矩阵用于自相关分析时,能够得出经济水平相近区域观测值的相似性,本文称其为“经济相关性”。这是对传统的“空间相关性”的扩展,正的经济相关性表明经济发展水平相近的区域的观测值相似,即观测值的分布表现出经济聚集的特征,负的经济相关性表明经济水平相近的区域的观测值趋异。
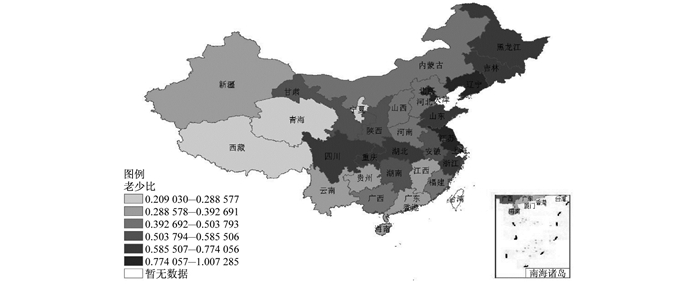
五 实证分析本文运用空间自相关模型和经济自相关模型对中国31个省份(不包括港、澳、台地区)2011年的老少比数据进行实证分析。通过ArcGIS软件,将全国31个省份的老少比指标按照数值大小(数值越大颜色越深)描绘在图 5中。
|
图 5 2011年中国老少比的分布状况 |
分别使用地理坐标和经济坐标按距离标准构建两个不同的一阶二元空间权重矩阵。在确定地理坐标时,利用ArcGIS软件确定全国31个省份的质心,并将各省份质心的经度和纬度作为其地理坐标,然后测算出坐标点间的球面距离,若距离在690.6英里范围内(这是软件测算的使每个位置至少有一个邻居的门槛距离),则认为两者相邻,在空间权重矩阵中对应的值为1;否则为不相邻,矩阵中对应的值为0。在确定经济坐标时,将各省份的GDP除以地区GDP的均值作为各省份的X坐标值,将各省份的CPI除以地区CPI的均值作为各省份的Y坐标值,然后测算出坐标点间的欧式距离,若其在0.75(门槛距离)的范围内,则相邻,否则为不相邻。
(二) 省域老少比的全局自相关通过GeoDa软件,分别使用地理坐标和经济坐标在距离标准下构建空间权重矩阵,计算并检验全局Moran′s I指数,结果如表 2所示。由表 2,度量空间相关性的全局Moran′s I为0.274,是一个显著的正值,表明全国31个省份的老少比存在全局空间正相关性。即从全国来看,老少比存在高高聚集或者低低聚集的模式,地理位置相近的省份老龄化程度比较接近。例如山东、江苏、上海和浙江等相邻地区的老龄化程度都很高,而青海、西藏和新疆等相邻地区的老龄化程度都很低。度量经济相关性的全局Moran′s I为0.391,也是一个显著的正值,表明从全国来看,经济水平相近的地区具有相似的老少比。例如北京、上海等经济发达地区的老龄化程度相近且偏高,而贵州、江西和宁夏等经济不发达省份的老龄化程度相近且偏低。而且衡量经济相关性的Moran′s I指数值大于衡量空间相关性的Moran′s I指数值,表明全国范围内老少比对经济水平的依赖性大于对空间位置的依赖性,老少比的经济聚集特征较空间聚集特征更为明显。
| 表 2 省域老少比的全局自相关性 |
1.局部Moran指数和局部G系数。利用两个不同的空间权重矩阵,分别测算省域老少比的局部自相关性。受篇幅所限,本文仅列出显著的、代表性省份的估计结果。基于地理坐标测算的局部自相关指标见表 3,基于经济坐标测算的局部自相关指标见表 4。
| 表 3 基于地理坐标的局部自相关指标 |
| 表 4 基于经济坐标的局部自相关指标 |
由表 3,北京、天津、辽宁、江苏和西藏的局部Moran指数显著为正,表明它们与周边省份的老少比有局部的空间正相关性,即它们和周边省份的老少比是高高聚集或低低聚集。同时,北京、天津、辽宁、江苏的局部G系数较高,说明这四个省份的老少比都是高高聚集模式。老少比分布图(见图 5)显示这四个省份周边区域的颜色较深,表明老少比都较高,故现实的分布情况与局部自相关分析得出的结论一致。而西藏的局部G系数为-1.858,是最低的,表明它与周边省份是低低聚集模式,即西藏与周边省份的老少比都较低。由图 5也可以看出,西藏、新疆、青海、云南等地的老少比的确较低。值得说明的是,局部G系数要结合显著的局部Moran指数进行分析,才能得出较可靠的结论。以局部Moran指数不显著的重庆为例来说明,重庆的局部G系数为-2.29,若不考虑其Moran指数是否显著时,就会得出重庆被低值区域包围的结论,然而实际情况是,重庆周围的四川、湖北、湖南等省份的老少比偏高,与局部自相关分析得出的结论不符,故对局部G系数的分析要在局部Moran指数显著的基础上进行,其结论才会与实际相符。
经济坐标用地区人均GDP和地区CPI来确定。从表 4中可以看出,基于经济坐标的测算得到了更多显著的局部Moran指数。其中,北京、上海具有较高的局部Moran指数,分别为3.440和3.595,表明局部存在较强的正向经济相关性,即与它们经济发展水平相当的省份拥有相似的老少比。同时,北京、上海的局部G系数较大,说明与其经济发展水平相近的省份有较高的老少比。由图 5,天津、辽宁、江苏和浙江大多是与北京、上海经济发展水平相近的沿海省份,它们也都有较高的老少比。而西藏、青海和新疆等地的局部Moran指数虽然也是显著的正值,但数值不大,故存在一定的经济相关性。西藏、青海和新疆等地属于经济不发达的地区,它们的老少比都很低。另外,经济发展水平相近的云南、贵州、广西、海南等地,其老少比也偏低。
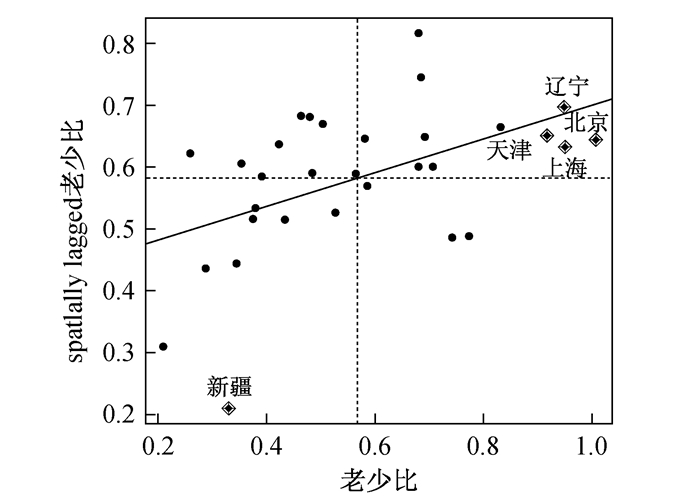
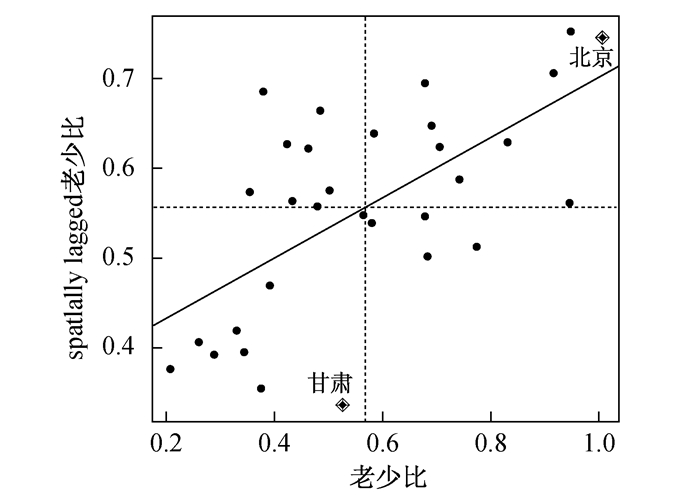
2. Moran散点图。基于地理坐标得到的Moran散点图如图 6,基于经济坐标得到的Moran散点图如图 7。从图 6可以看出,对老少比的空间分布有重大影响的省份有北京、上海、天津、辽宁和新疆,其局部Moran指数值都较大,对全局的Moran′s I值有很大的影响。其中北京、上海、天津、辽宁位于第一象限,表明这些省份都具有较高的老少比,且被老少比较高的省份所包围,即局部呈现出高—高模式。而新疆处于第三象限,表明其老少比很低,且被老少比较低的省份所包围,即局部呈现出低—低模式。从散点图中还可以看出,我国31个省份中大多数省份的老少比分布在第一、二、三象限,位于第四象限的很少,说明大多数省份的局部空间分布主要呈现高—高、低—高、低—低的特征。由图 7,全国31个省份的老少比也主要分布在第一、二、三象限,即分布类型仍然主要为上述三种模式。其中有重大影响的省份为北京和甘肃。北京位于第一象限内,说明其老少比很高,且与其经济发展水平相近的区域如天津、江苏、上海等地的老少比也很高。甘肃位于第三象限内,说明其老少比较低,与其经济发展水平相近的区域如贵州、新疆等地的老少比也偏低。
|
图 6 基于地理坐标的Moran散点图 |
|
图 7 基于经济坐标的Moran散点图 |
本文根据全国第四、五、六次人口普查数据以及《中国统计年鉴》(2012)中的相关数据,分析我国人口老龄化现状以及老龄化趋势和经济发展趋势之间的关系,并进一步采用空间自相关模型和新构的经济自相关模型,用全局Moran′s I指数刻画全局自相关,用局部Moran指数和局部G系数刻画局部自相关,分别研究中国各省份老龄化的空间和经济相关性,得到以下主要结论:
第一,无论是老年人口比例、老年人口抚养比还是老少比,我国绝大多数省份都已达到或远远超过国际的老龄化标准,是老龄化较严重的国家之一。同时我国人口分布不均匀,各省份的老龄化程度差异较大。纵观1990—2010年,我国各省份的老龄化程度都在逐渐加深中,且速度较快,正在经历高速的老龄化进程,人口发展前景令人担忧。
第二,从老少比和人均GDP的关系上来看,北京、天津、上海、江苏、浙江、山东的老龄化程度和经济发展水平大致相当,而全国绝大多数省份的人口老龄化都一直超前于经济发展,长期对经济发展形成压力,属于典型的“未富先老”型。
第三,空间自相关性的显著Moran′s I指数值为0.274,表明从全局来看,中国老龄化存在一定程度的空间聚集特征,即地理位置相近的省份老龄化程度接近。而经济自相关性的显著Moran′s I指数值为0.391,表明中国老龄化存在一定程度的经济聚集特征,即经济发展水平相近的省份老龄化程度接近。而且经济相关性大于空间相关性,说明老少比这一指标对经济发展水平的依赖性大于对空间位置的依赖性。从局部来看,局部经济自相关中有显著Moran指数的省份的数量较局部空间自相关中的多,即老龄化的地区差异中经济发展水平较空间位置的影响更甚。
由于我国老龄化水平存在区域差异,在一定程度上依赖于经济水平的发展,因此,应根据经济发展水平进行区分,因地制宜地制定老龄化的应对策略。如在经济较为落后的地区,提高基本养老金整体水平,保障老年人的生活,推动和发展老年文体活动,进一步完善养老制度以及各项社会福利;而在经济较发达的地区,适时、灵活、稳健地调整人口生育政策,尽快实现从“一对夫妇生育一个孩子”向“单独两孩”的过渡,使我国的实际生育率略有上升,接近人口生育更替水平,逐步实现少儿人口、青年人口、劳动年龄人口以及总人口规模的稳定。
包玉香, 2012, 《人口老龄化的区域经济效应分析——基于新古典经济增长模型》, 《人口与经济》第1期。 |
陈茗, 2001, 《人口老龄化的区域差异和形成要因的中日比较分析》, 《人口与经济》第S1期。 |
胡鞍钢、刘生龙、马振国, 2012, 《人口老龄化, 人口增长与经济增长——来自中国省际面板数据的实证证据》, 《人口研究》第3期。 |
李本公, 2006, 《中国人口老龄化发展趋势百年预测》, 北京: 华龄出版社。 |
林琳、马飞, 2007, 《广州市人口老龄化的空间分布及趋势》, 《地理研究》第5期。 |
刘爽, 1997, 《对中国区域人口老龄化过程的思考》, 《人口学刊》第3期。 |
王泽宇、孙然、韩增林、刘凤朝, 2013, 《中国人口老龄化水平测度与空间关联研究》, 《地域研究与开发》第3期。 |
邬沧萍、王琳、苗瑞凤, 2004, 《中国特色的人口老龄化过程, 前景和对策》, 《人口研究》第1期。 |
袁俊、吴殿廷、吴铮争, 2007, 《中国农村人口老龄化的空间差异及其影响因素分析》, 《中国人口科学》第3期。 |
查奇芬、谢明柱, 2013, 《农村人口老龄化空间格局及影响因素研究》, 《湖南农业大学学报(社会科学版)》第4期。 |
张晓青, 2009, 《新世纪以来中国人口老龄化研究的新动向》, 《人口与发展》第3期。 |
赵儒煜、刘畅、张锋, 2012, 《中国人口老龄化区域溢出与分布差异的空间计量经济学研究》, 《人口研究》第2期。 |


