行业收入差距长期稳定存在,泰勒(Thaler,1989)称之为跨职业工资差异稳定性,大量的实证研究支持这一结论。Krugeger和Summers(1988)使用美国人口调查数据(CPS)分析发现,在控制了教育水平和经验等人力资本因素后,仍然存在未被解释的行业工资差异;即使剔除不可观察的人力资本因素(如遗传因素)的影响,同一人在不同行业间转换工作后,该结论仍然成立。
行业收入差距理论包括竞争性劳动力市场理论、人力资本理论、效率工资理论、工会威胁模型和垄断租金分享理论。新古典分析框架下的竞争性劳动力市场理论包括短期差异理论和补偿性差异理论,前者认为产品需求暂时性增加的行业倾向于支付较高的行业工资,以吸引更多的劳动力(Arbache,2001);后者强调部分行业具有降低劳动者效用水平的不利特征(劳动强度高或工作环境差),需要对劳动者进行额外补偿(Schettkat,1993)。人力资本理论认为,行业收入差距可以由劳动者人力资本水平(如教育程度、健康水平等)来解释,高收入行业往往拥有更多高质量的劳动力(Martins,2004)。效率工资理论强调在信息不对称行业如何配置资源、提高劳动生产率(Dickens & Katz, 1987)。工会威胁模型认为工会能够帮助会员工人通过集体行动、罢工、怠工等方式将工资提高到竞争性工资水平以上,工会力量越强,行业收入可能越高(Freeman et al., 1984)。垄断租金分享理论认为具有垄断势力的企业在攫取超额利润时,管理层和普通员工也能够分享一部分超额报酬(Nickell,1999)。由于我国与西方国家经济体制不同,国内学者侧重于分析行业垄断,尤其是行政垄断对行业收入差距的影响(张龙等,2015)。
在理论上,教育对收入差距的影响没有统一定论。最初的人力资本理论(Schultz, 1960;Mincer, 1974;Becker, 1975)认为教育作为最重要的人力资本积累手段,与收入不平等之间存在着稳定的密切关系,通常教育不平等与收入不平等正相关。奈特和萨伯特(Knight & Sabot,1983)强调,在二元经济中由于教育存在结构效应和工资压缩效应,人力资本积累对收入分配有着复杂的影响;教育发展的结构效应使收入差距扩大,其抑制作用可以缩小收入差距。国内学者从不同角度进行的实证研究,也未能就此达成一致结论。白雪梅(2004)使用我国1982—2000年的时间序列数据,发现教育不平等会加剧收入不平等;杜鹏(2005)利用我国1995—2002年的教育和收入分配数据,发现教育拓展随着教育年限的延长扩大了居民收入差距,教育分布的平等化并没有改变这一趋势,教育平等化对收入差距的影响在我国并不明晰。龙翠红(2011)发现,收入分配差距导致教育不平等,改进教育不平等却没能改善收入分配差距,我国教育平等与收入平等双向的良性循环还未形成。
有关人力资本影响行业收入差距的文献,按行业收入差距的测量方法可分为两类。一是用行业收入替代行业收入差距,本质上是研究行业收入。这类研究论证途径与目标不一致,试图将教育对行业收入的影响转移到行业收入差距上,但揭示的仍是教育与行业收入的关系。例如张原等(2008)发现受教育年限对中国行业工资回报具有正向作用,得出人力资本能够解释我国行业间工资回报差异的结论;张世银等(2010)以行业人均工资为被解释变量,发现人力资本水平扩大了行业收入差距;葛晶等(2016)认为行业垄断吸引人力资本,推升了行业收入,由此间接推断出行业垄断扩大了行业收入差距。第二类研究避开了这种误区,采用相对更合理的指标测算行业收入差距。葛玉好等(2015)认为行业间的公平并不意味着收入均等化,并借鉴狄更斯和卡茨(Dickens & Katz,1987)的方法,以同一职业在不同行业间的收入差异程度来测度行业收入差距,发现人力资本理论能够部分地解释“各类专业技术人员”的行业收入差距,但不能解释“国家机关、党群组织和企事业单位负责人”的行业收入差距。此种方法比较的是某类职业(如管理型人员、专业技术人员)在不同行业间的收入差异,而非常规统计口径的行业收入差距。部分学者采用各行业平均工资与全部行业平均工资的比值来度量行业收入差距。王敬勇(2013)使用1992—2010年19个A类行业的面板数据,讨论了行业垄断、人力资本和两者的交互作用对行业收入差距的影响,发现人力资本(教育年限)对行业收入差距的影响具有倒U形的非线性特征,但总体而言人力资本提升扩大了行业收入差异。邱兆林(2014)通过区分三种不同质量的人力资本,发现在非垄断行业只有具备达到一定质量的人力资本才能扩大行业收入差距,在垄断行业低质量和高质量的人力资本都会拉大行业收入差距,但该研究没有给出人力资本(教育年限)对行业收入差距的综合影响。
各行业平均工资与全部行业平均工资的比值在一定程度上能够测度行业间的收入差距,但相比行业基尼系数和行业泰尔指数仍显得较为粗糙。良好的收入差距测度指标需具备匿名性、齐次性、总体独立性、转移性和强洛伦兹一致性(万广华,2008),基尼系数和泰尔指数均能满足上述要求。但采用行业基尼系数或行业泰尔指数研究教育与行业收入差距关系的文献屈指可数。王涛(2014)基于19个A类行业的泰尔指数,研究了行业收入差距与经济增长的关系,但没有分析教育对行业收入差距的影响。宗振利等(2013)基于2003—2010年的省际面板数据,发现提高行业人力资本水平可以明显缩小行业收入差距,但模型的估计方法没有考虑地区的空间相关性,忽略了地理因素对行业收入差距的影响。王雪辉(2016)运用空间计量模型研究发现我国的地区工资具有明显的空间依赖关系。吴晓怡等(2016)将空间经济学分析方法应用到行业收入的研究中,发现经济集聚与制造业行业工资差距具有倒U形关系,但忽视了地区工资收入的空间相关性。
本文的贡献首先在于,以2003—2013年各省份97个行业的工资统计数据为基础,计算行业基尼系数和行业泰尔指数,数据更全面,指标更合理;其次在研究方法上,使用空间面板计量方法研究人力资本与行业收入差距的关系,不但引入了产业集聚等地理变量,同时克服了空间相关性问题,因而估计结果更精确。由于指标和研究方法更合理,本文发现了教育扩大行业收入差距的多种证据。目前中国刚达到中等收入水平,收入差距悬殊,学区房和留学热等现象都是教育扩大收入差距的表象。
二 行业收入差距和人力资本的演化趋势 (一) 行业收入差距的度量1.行业平均工资基尼系数(gini),简称行业基尼系数或基尼系数。按照Sen(1973)的公式计算:
| $ gini{\rm{ = 1 + 1/}}N{\rm{ - 2/}}{N^{\rm{2}}}\mu \sum\limits_i^n {\left( {n + 1 - i} \right){y_i}} $ | (1) |
其中,μ为所有行业的平均收入,yi为行业i的平均行业工资,N为行业总数。
2.行业平均工资泰尔指数(theil),简称行业泰尔指数或泰尔指数。由广义熵指数转化而来,广义熵指数G(α)为:
| $ G\left(\alpha \right) = \left({1/\alpha \left({\alpha - 1} \right)} \right)\left({{w_i}\sum\limits_i^N {{{\left({{y_i}/\overline y } \right)}^\alpha } - 1} } \right) $ |
其中:
| $ theil{\rm{ = }}G\left(1 \right) = \frac{1}{n}\sum\limits_{i = 1}^n {{w_i}\left({\frac{{{y_i}}}{{\overline y }}\log \frac{{{y_i}}}{{\overline y }}} \right)} $ |
3.数据及行业收入差距的演化趋势。2003年国家统计局实行“国民经济行业分类”新标准,所以本文的样本时间为2003—2013年。基于数据可得性,本文选择A类(大类)19个行业和混合行业两种数据口径。混合行业包括工业二位数行业39个,服务业49个,第一产业的农、林、牧、渔及服务5个行业,再加上党、政、政协和民主党派及社团4个行业,共97个行业。本文数据来自历年《中国统计年鉴》和《中国劳动统计年鉴》。
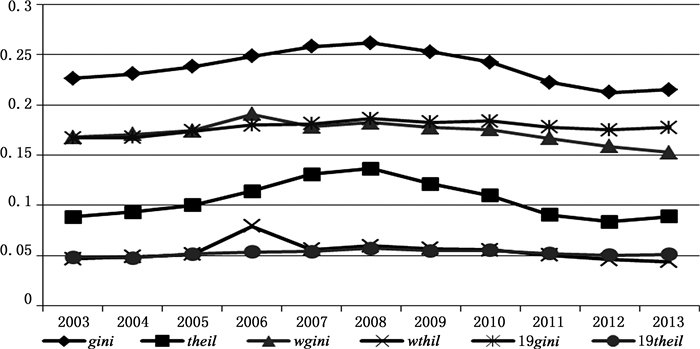
(1) 全国行业收入差距演化趋势。从图 1可以看出①,19个行业以及加权的基尼系数及泰尔指数波动很小,所以混合行业的泰尔指数和基尼系数是本文行业收入差距的主要测度指标。泰尔指数和基尼系数具有明显倒U形时间特征,先上升后下降,拐点在2008年。
|
图 1 2003—2013年全国行业收入差距 |
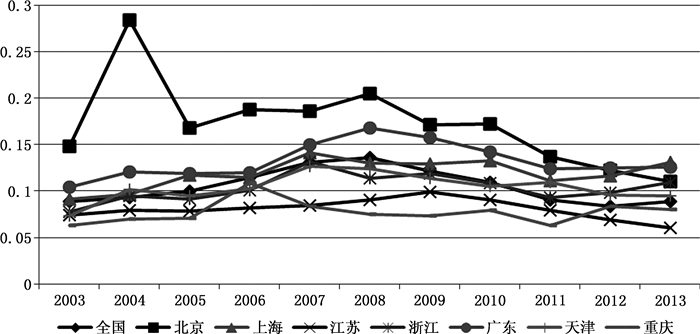
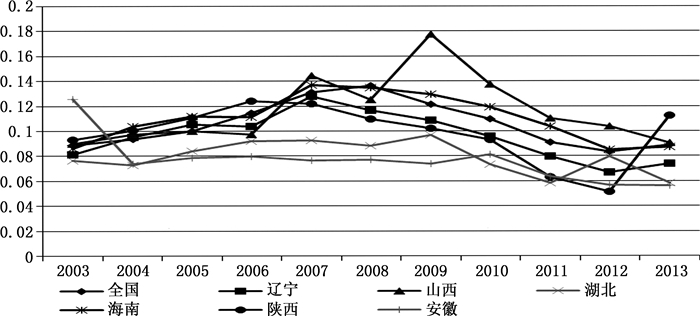
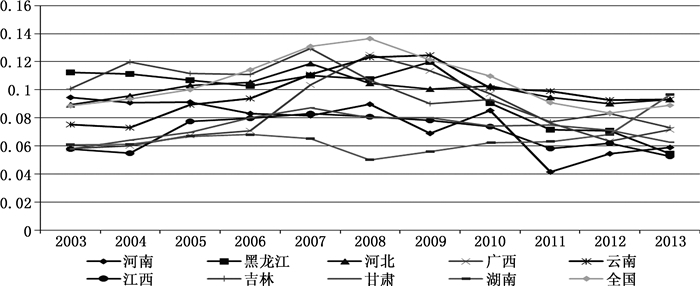
(2) 行业收入差距的地区异质性。为观察地区行业收入差距的发展趋势,按2014年各地区城镇居民人均工资收入①的25%分位数和75%分位数将全国31个省份分为高、中等和低收入地区(见表 1)。以泰尔指数为例(图 2—4),高收入地区的行业收入差距最大,其次为中等收入地区和资源型地区,如山西。江苏和重庆的行业收入差距比较稳定,工资收入较高,行业收入差距较小。
| 表 1 地区收入分组 |
|
图 2 部分高收入地区的泰尔指数 |
|
图 3 部分中等收入地区的泰尔指数 |
|
图 4 低收入地区的泰尔指数 |
与高收入地区类似,中等和低收入地区的行业收入差距基本也呈倒U形分布,例外地区为安徽和湖南,为U形趋势。河南的行业收入差距持续下降,黑龙江、云南、吉林和河北的行业收入差距接近高收入地区的平均水平,是典型的低收入和收入严重不均等地区。观察图 2—4,中等收入地区的行业收入差距有发散趋势,而高收入地区和低收入地区的行业收入差距则逐渐收敛。
(二) 人力资本:教育程度(edu)1.教育程度的度量。如何度量人力资本或教育程度,目前学术界没能达成一致,部分学者选择中高等学校在校生人数作为代理变量(刘修岩等,2007;张文武等,2011)。鉴于毕业生流动性较强,该指标并不合适。当受教育程度提高时,本地区的人力资本数量也上升,受教育程度既能反映人力资本质量也能体现数量。本文以受教育年限为地区人力资本或教育程度的代理变量。借助《中国劳动统计年鉴》的地区就业人员学历占比数据,其计算公式如下:
| $ ed{u_i}{\rm{ = }}\sum\nolimits_h {{\omega _{ih}}yea{r_{ih}}} $ | (2) |
其中,edui为地区i的人力资本平均受教育年限;h为学历类型,分别为学前、小学、初中、高中、大专、本科和研究生学历;ωih为i地区的h类型学历就业人员占本地区的比例;yearih为h类型学历的学习时间。按惯例,学历时间分别设为0、6、9、12、15、16、19年。
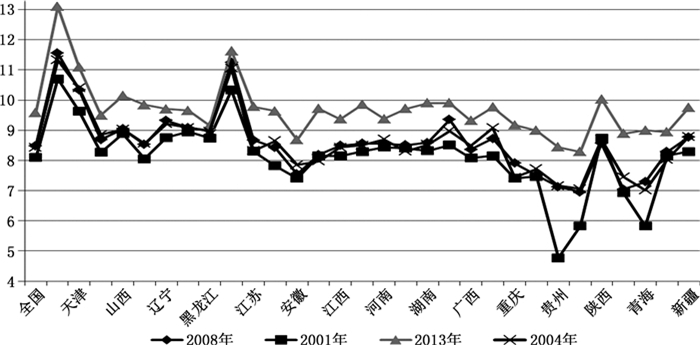
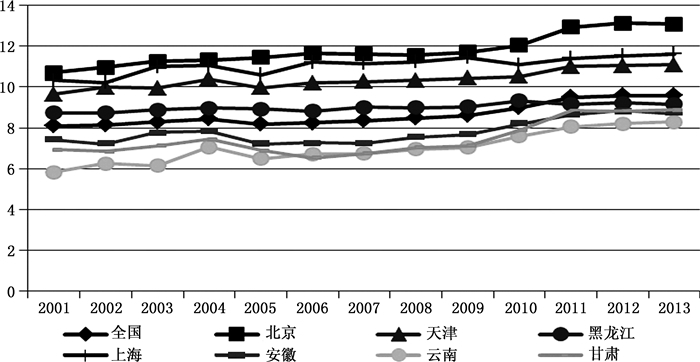
2.教育年限的趋势和地区特征。如图 5,中国平均受教育年限由2001年的8.1年提高到2013年的9.7年,受教育程度明显提高。与基尼系数和泰尔指数具有空间异质性不同,各省份的教育年限在时间上具有高度趋同性。根据图 6,北京的教育程度最高,其次为上海和天津;安徽、云南和甘肃的教育年限低于全国平均水平。教育程度的地区差异在时间上几乎不变,只有2001年教育年限的地区差异与其他年份略有不同。贵州、云南、甘肃和青海明显偏低,但到2004年差距已经显著缩小。各省份的教育程度逐年提高,2013年比2008年教育年限有明显提升,而2001—2008年受教育年限增长缓慢。
|
图 5 教育年限的地区差异 |
|
图 6 教育年限的时间趋势 |
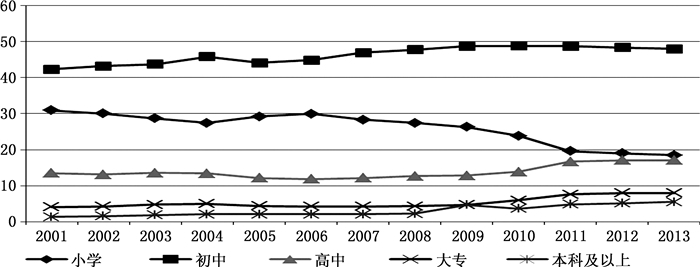
3.学历构成。图 7给出了中国就业人员的学历占比。大部分就业人员的学历为初中,其次为小学,大专和本科的学历占比不超过10%。从2009年开始,就业人员的学历构成发生了明显变化,小学学历就业人员明显下降,高中上升,大专和本科以上学历略有增长,初中学历占比稳定。
|
图 7 学历构成 |
根据前文分析,地区和行业间的工资具有传递性,可能存在空间依赖关系。基于面板数据的空间滞后模型(SLM)和空间误差模型(SEM),可以描述具有空间依赖性个体的变化规律。但在设定空间经济计量模型之前,还需要对被解释变量行业收入差距进行空间效应检验。
(一) 空间相关性分析本文通过Moran's I指数检验行业收入差距的空间相关性。根据表 2,gini系数的Moran's I值均通过了1%的显著性检验①,某一地区的行业收入差距受本地区和周边地区的共同影响,中国的地区行业收入差距具有空间效应。
| 表 2 2003—2013年中国行业gini的Moran's I及相应的P值 |
1.空间滞后模型。空间滞后模型(SLM)即空间自回归模型(SAR),适用于研究空间中某地区的经济变量受其临近地区经济变量溢出的影响,即空间自相关。设定SLM模型如下:
| $ gini = \rho Wgini + X\beta + \mu + \lambda + \varepsilon $ | (3) |
其中,W为N×N阶空间权重矩阵;X为包含edu及控制变量的向量矩阵,ρ为空间自相关系数;β为参数向量,ε为随机误差向量,N为地区数量。μ和λ表示特定的空间和时间效应。模型还需通过Hausman检验以选择固定效应或随机效应估计方法。
2.空间误差模型。空间误差模型(SEM)也强调地区的随机冲击对邻近地区的传递效应,被解释变量本身不具有空间相关性。其权重矩阵可以与空间滞后模型相同或不同,本文为保持空间模型的完整性和一致性,对两者采用相同的权重矩阵。
| $ gini = X\beta + \mu + \lambda + \varepsilon, 其中\varepsilon = \rho W\varepsilon + \tau $ | (4) |
(4) 式中,τ是服从正态分布的随机误差向量,ρ为解释变量空间误差自相关系数,其余同(3) 式。
(三) 权重矩阵估计(3) 式和(4) 式,需要设定表征空间单元之间的相互依赖与关联程度的空间权重矩阵W。产业在空间集聚的过程中对地区和行业工资差距的影响不仅依赖于地理因素,还通过经济发展水平的空间依赖性相互间发生作用。设定空间权重矩阵如下(刘瑜等,2014):
| $ {w_{ij}} = C{P_i}{P_j}f\left({{d_{ij}}} \right) $ | (5) |
其中,wij是W的i行j列权重系数,表示地区i和j之间的相互作用强度;C为常量系数;Pi和Pj是GDP规模;f(dij)是地区之间距离的衰减函数,函数形式选择负幂律函数。
(四) 重要控制变量:产业集聚度和市场潜能劳动生产率是人力资本或教育程度的重要控制变量,已有研究通常选择全要素生产率为生产效率的代理变量(邱兆林,2014)。新经济地理学将垄断竞争、运输成本和规模收益递增联系起来,深入探究了经济活动的空间分布规律和空间集聚特征。该理论已成为地区收入差距研究的重要理论基础,如Fingleton(2006)、刘修岩(2007)等。资源根据市场潜力进行空间配置,推动了产业在行业间的转移,促进了产业结构的调整。要素的空间转移和行业重新配置导致某些产业在新的地区聚集,推升了该行业的工资。地区性的产业集聚和市场潜能同时影响地区和行业间的收入差距,产业集聚理论指出了行业收入差距的微观机制,即竞争的方式或效率的来源。
1.产业集聚程度。区位熵是产业集聚的常用指标(刘军等,2010)。区位熵可以消除区域规模的差异因素,反映地理要素的空间分布。鉴于2015年我国服务业占比已超过50%,本文以制造业和服务业的集聚程度反映产业结构的空间特征。对制造业集聚度定义如下:
| $ inma{g_i} = \left({{\theta _i}/\sum\nolimits_j {{\theta _{ij}}} } \right)/\left({\sum\nolimits_j {{\theta _{ij}}/\sum\nolimits_i {\sum\nolimits_j {{\theta _{ij}}} } } } \right) $ | (6) |
其中,inmagi表示地区i的制造业集聚度,θi代表地区i制造业增加值,θij表示地区i产业j的增加值。服务业集聚度(sermagi)的定义类似。
2.市场潜能。市场潜能在一定程度上反映地区可获得的整体市场规模,借鉴Harries(1954)的“市场潜能函数”,对市场潜能mpi定义如下:
| $ m{p_i} = \sum\nolimits_{i \ne k} {{Y_k}/{d_{ik}} + {Y_i}/{d_{ii}}} $ | (7) |
其中,Yi为地区i的生产总值;dik为地区i与k间的欧式直线距离①,本文使用国家基础地理信息系统地形数据库,通过Arcview3.3软件计算dik;借鉴刘修岩(2007)的研究,本文将内部距离dii定义为:dii=(2/3)
很多国有企业处于竞争性行业(如海尔、格力),国有化比重和市场集中度不是合适的垄断性指标。石油及天然气开采业、交通运输仓储及邮政业、水电力热力和供应业、金融业、烟草加工业等行业存在准入门槛,为典型的垄断行业,本文以五大行业的产值占地区生产总值的比例度量垄断程度。Kuznets(1955)指出,随着收入增长,收入差距将先上升后下降,此即库兹涅兹倒U曲线假说,因此人均GDP是不可忽视的控制变量。中国的进出口与外资相关,外资占GDP比例较高的行业工资收入也较高。外资根据市场潜能进行地区和行业选择,促进了地区的产业集聚水平。本文以各地区的FDI占GDP的比例作为市场开放度的代理变量。
(六) 变量的统计描述根据表 3,泰尔指数的标准差远大于基尼系数,更能反映行业收入差距的时间趋势。山西2008年的泰尔指数为1.305,部分原因是原材料价格上涨导致煤炭等相关行业收入较高。为降低异常值的影响,在图 3、表 3和模型估计时作了平滑处理。图 1—5的其他数据没有异常值。
| 表 3 变量的统计描述 |
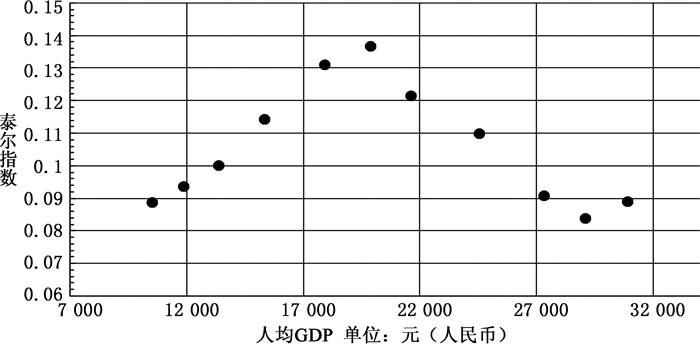
1.模型的函数形式。如图 8,泰尔指数(基尼系数类似)与人均GDP呈非线性关系,类似库兹涅茨倒U形曲线。行业收入差距随着经济发展先升后降,空间回归模型应引入人均GDP的平方描述这种非线性关系。行业收入差距与人均GDP是否具有倒U形关系,需要控制其他变量的影响,才能得到验证。
2.模型估计结果。由上文可知,产业集聚与地区工资具有显著的空间相关性,只从经济学角度分析可能会忽略地理特征,难以全面揭示工资及工资差距的作用机制和空间影响。如表 4,Hausman检验结果表明各模型更适合使用固定效应估计法。OLS模型由于忽略地区之间的相关性,参数估计产生了严重的偏误,只有教育年限和人均GDP两个变量显著,拟合优度也明显低于空间模型。而空间滞后模型和空间误差模型对ρ的估计值为正,符合预期,误差项和滞后项都通过了1%的显著性检验,模型通过了空间自回归的LR和LM检验。
| 表 4 基尼系数模型估计结果 |
SLM和SEM模型表明,行业收入差距本身不但具有空间之间的交互作用,而且对地区间的截面个体发生的冲击也会传递到相邻的个体,例如北京、上海和深圳的房地产业冲击会传递到相邻地区,产生溢出效应。根据表 4的估计结果,影响行业收入差距的主要因素是教育年限、服务业集聚水平、市场潜能、开放程度和行业垄断程度,它们与行业收入差距在统计上显著正相关。
(二) 模型分析 1. 教育的行业收入差距扩大效应根据表 4,教育年限(edu)的参数符号为正,且在1%的显著性水平下显著,表明随着教育年限的增长,行业收入差距逐渐扩大。宗振利等(2013)采用差分广义矩估计法,利用2003—2010年的面板数据得出了相反的结论;其回归模型的行业收入差距和教育变量含义与本文完全相同,只有部分控制变量不同。
为进一步说明教育对行业收入差距的影响机制,用学历构成代替教育年限估计SEM模型,简称学历模型。学历构成变量包括各学历就业人数占全部就业人数的比例,分别简称为小学学历占比、初中学历占比、高中学历占比、大专学历占比、本科以上学历占比。①根据学历模型,中国各省份的小学和大专学历占比提高会缩小行业收入差距(参数估计值为负数),其他学历占比上升则会扩大行业收入差距。学历模型表明教育对行业收入差距的影响具有结构效应,不同学历占比上升对行业收入差距的影响不同。由于小学学历占比与行业收入差距负相关,且从2001—2013年持续下降(见图 7),那么小学学历占比下降产生了扩大行业收入差距的效应。
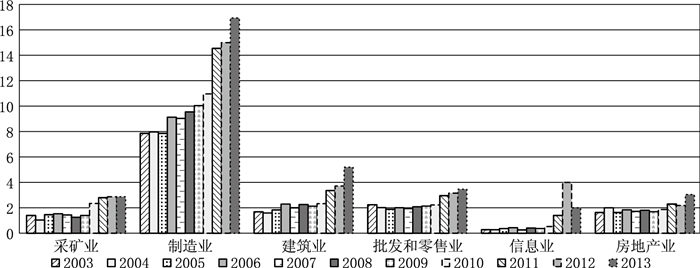
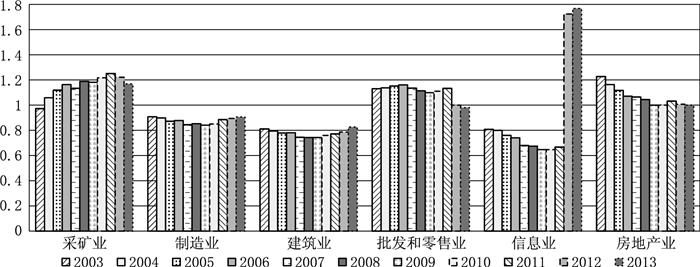
大专学历占比最高的行业是教育行业,其占比由2003年的39%下降到2013年的17.36%;同期教育行业的平均收入与全国平均收入比由1.04下降到0.86。大专学历占比上升的行业为采矿业、制造业、建筑业、批发和零售业、信息传输软件及技术服务业(信息业)、房地产业,如图 9。在这6个行业中,制造业大专学历占比由2003年的6.49%上升到了2013年的16.91%,增长最快。从2008年开始,制造业大专学历就业人员增速明显提高,同时制造业相对工资也开始上升,与优势行业的工资差距缩小。根据图 10,制造业、建筑业、批发零售业、信息业的行业人均收入都低于全国平均收入水平,为低收入行业。大专学历就业人员涌入低收入行业,提高了行业效率和行业工资水平,产生了缩小行业收入差距的效应。
|
图 9 各行业大专学历就业人员占比 |
|
图 10 行业人均收入/全国平均收入 |
根据图 6和图 7,中国就业人员的小学学历占比下降、初中学历占比略微上升和其他三种学历占比上升共同提高了就业人员的受教育年限。小学学历占比下降产生了扩大行业收入差距的效应,初中、高中和本科以上学历占比与行业收入差距正相关,三种学历占比上升扩大了行业收入差距。大专学历占比增长幅度不大,大专学历占比提高对行业收入差距唯一的缩小效应难以抵消其他四类学历占比变化带来的扩大效应。
观察图 1,行业收入差距的拐点在2008年,2008—2012年泰尔指数下降了11.8%。学历构成的两种正负效应在2008年前后产生的总效应可能会不同,教育和行业收入差距可能存在非线性关系,尽管在样本期内总效应为扩大效应。根据表 4的教育(edu)非线性模型,教育年限和行业基尼系数存在倒U形关系,行业收入差距随教育年限的增长而先上升后下降,这一结论与王敬勇(2013)的研究类似。在总趋势上,教育年限和行业收入差距正相关,本文在第五部分将进一步提供教育年限与行业收入差距正相关的其他证据。
2. 新经济地理学对行业收入差距的解释能力根据表 4,市场潜能和服务业集聚度与行业收入差距显著正相关①,表明新经济地理学对行业收入差距有解释力。服务业集聚度的影响超过工业有三点原因。第一,从2012年开始服务业超过工业成为最大产业;第二,中国大部分地区的工业发展水平具有趋同性或同质性;第三,工业内部的行业收入差距明显低于服务业。2008年工业行业中收入最高行业——烟草业的人均工资是其最低行业——木材加工业的人均工资的3.83倍,同期证券业的人均工资是餐饮业的人均工资的9.5倍。邻近经济核心圈的地区市场潜能较大,运输成本低,规模效应明显,行业工资较高。东部地区的市场潜能加速了服务业和高端制造业崛起,高级人才集聚推升了行业工资;中西部地区的资源行业凭借市场潜能优势其工资增长快于其他行业。
3. 库兹涅兹效应根据表 4的人均GDP线性模型,行业收入差距随人均GDP的增加而减少,即行业收入差距随人均GDP的提高呈下降趋势。这符合2008—2013年行业收入差距明显下降的事实,见图 8。人均GDP的非线性模型表明,行业收入差距先上升后下降,随着人均收入的持续增加,行业收入差距最终下降。行业收入差距与人均GDP在1%的水平上存在类似“库兹涅兹曲线”的倒U形关系,提示了经济发展过程中收入差距的一般变化规律。
|
图 8 泰尔指数与人均GDP散点图 |
为检验结论的稳健性,用泰尔指数代替基尼系数,解释变量不变,重新估计(3) 式和(4) 式,估计结果见表 5。与表 4的估计结果类似,OLS模型的估计精度低于空间模型。根据SEM模型,受教育年限和行业收入差距仍然正相关,教育的结构效应、非线性特征与表 4相对应的模型相同。其他变量的估计结果与表 4类似,学历变量的参数估计值省略。
| 表 5 泰尔指数模型估计结果 |
根据图 1,行业收入差距从2008年开始下降,2011年趋缓,2013年开始上升。2008年底开始的大规模刺激政策在2011年后逐渐退出,2013年又加码,政策时间点与行业收入差距的演变正好匹配。调控政策与行业收入差距的呼应绝非偶然,本部分将从时间和截面样本进一步展开讨论。
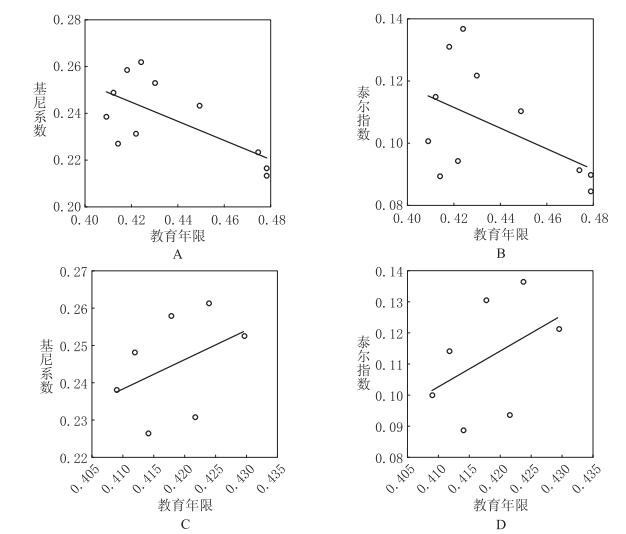
(一) 时序样本分析为进一步分析教育对行业收入差距的影响,图 11给出了教育与行业收入差距2003—2013年(图A和B)和2003—2010年(图C和D)的散点图。根据图 11,2003—2013年教育年限与行业收入差距明显负相关,意味着提高教育年限能够缩小行业收入差距。但仔细观察图A与图B,教育的缩小效应由行业收入差距的三个较低点形成,这三个点分别对应2011—2013年。2011—2013年行业收入差距迅速下降,扭转了教育年限和行业收入差距的关系。如果将2011—2013年的三个点删除,得到图C与图D,可以发现教育与行业收入差距正相关。图C和图D包括11个年份中的8年,反映了教育与行业收入差距的大部分关系。那么我们可以认为,图A与图B的缩小效应是奇异值点造成的,对大部分样本而言行业收入差距与受教育年限正相关。
|
图 11 教育年限与行业收入差距的相关性 |
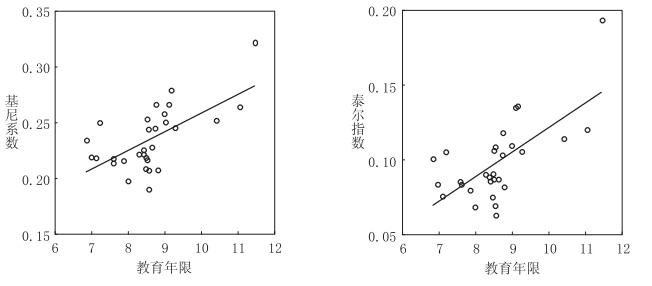
无论是固定效应还是随机效应,面板模型的参数刻画了变量在时间上的相关性。教育与行业收入差距的关系也可通过截面样本(省份)来估计,组间估计法通过计算各变量在时间上的均值得到截面样本,估计变量在截面间的相关性。组间估计法忽略了很多信息,但从另一角度反映了受教育年限与行业收入差距的相互关系。中国30个省份2003—2013年的平均教育年限和行业收入差距关系见图 12,无论是基尼系数还是泰尔指数,地区教育年限和行业收入差距明显正相关。
|
图 12 教育年限与行业收入差距(地区截面样本) |
分别以基尼系数和泰尔指数为被解释变量,采用组间估计法依次估计OLS、SLM和SEM三种模型,估计结果见表 6。由于组间估计法损失了大量样本信息,SLM和SEM的Wald和LM识别检验没有全部通过,SLM和SEM模型只是略优于OLS模型。在控制了fdi、gov和pgdp后,各模型教育年限(edu)的参数估计值都为正,且多数在统计上显著。基尼系数OLS和SLM模型的edu参数估计值虽然在统计上不显著,但t值都大于1;模型的核心控制变量sermag和mp及其他控制变量的参数符号都与表 4和表 5的模型一致。
| 表 6 截面样本模型的估计结果 |
平均而言,人均工资越高的地区行业收入差距越大。大部分地区行业收入差距在时间上呈现倒U形趋势,2008年行业收入差距达到最大值;行业收入差距存在明显的地区异质性。空间回归模型表明,教育与行业收入差距具有倒U形非线性关系;总体而言,教育扩大了行业收入差距,其他证据也支持这一结论,这与宗振利等(2013)的结论恰好相反。教育对行业收入差距的影响具有结构效应,大专学历占比提高缩小了行业收入差距,小学学历占比下降和其他三类学历占比上升都扩大了行业收入差距;大专学历占比提高对行业收入差距的缩小效应难以抵消其他四种学历占比变化带来的扩大效应,因此,中国就业人员的受教育年限上升总体上扩大了行业收入差距。行业收入差距与人均GDP存在着类似“库兹涅兹曲线”的倒U形关系,当人均收入较低时行业收入差距上升,随着人均收入的持续增加,行业收入差距将最终下降。
我们没有找到教育缩小行业收入差距的证据,空间回归模型分析、时序样本分析和截面样本模型的组间估计都支持教育扩大行业收入差距的结论。本文也尝试利用2003—2010年面板数据建立空间模型,其估计结果也支持教育扩大行业收入差距的结论。①宗振利等(2013)使用差分GMM估计方法,没考虑地区间的相关性,得出了教育缩小行业收入差距的结论,由此也可以说明,地区面板数据更适合使用空间计量方法。
| 白雪梅, 2004, 《教育和收入不平等: 来自中国的经验数据》, 《管理世界》第6期. |
| 杜鹏, 2005, 《我国教育发展对收入差距影响的实证分析》, 《南开经济研究》第4期. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFD2005&filename=NKJJ200504009&v=MTE0MzhNMUZyQ1VSTDJmWU9kbUZ5em5WcnZLS3liQlpMRzRIdFRNcTQ5RmJZUjhlWDFMdXhZUzdEaDFUM3FUclc= |
| 葛晶、周子栋, 2016, 《行业垄断、行业特征与行业收入差距——基于多层次线性模型的研究》, 《西安财经学院学报》第3期. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFDLAST2016&filename=SXGY201603006&v=MjA1NjVMMmZZT1J1RmlIZ1ZMekJOalhNZDdHNEg5Zk1ySTlGWW9SOGVYMUx1eFlTN0RoMVQzcVRyV00xRnJDVVI= |
| 葛玉好、李莹、杜慧超, 2005, 《中国城镇地区行业收入差距的测度及成因分析》, 《劳动经济研究》第4期. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFDLAST2015&filename=LDJJ201404006&v=MjI4MDk5WE1xNDlGWW9SOGVYMUx1eFlTN0RoMVQzcVRyV00xRnJDVVJMMmZZT2RtRnl6blY3L0FLU25CWkxHNEg= |
| 刘军、徐康宁, 2010, 《产业集聚、经济增长与地区差距》, 《中国软科学》第7期. |
| 刘修岩、贺小海、殷醒民, 2007, 《市场潜能与地区工资差距: 基于中国地级面板数据的实证研究》, 《管理世界》第9期. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFD2007&filename=GLSJ200709006&v=MjU2MTZWN3JMSWlIWVpMRzRIdGJNcG85RllvUjhlWDFMdXhZUzdEaDFUM3FUcldNMUZyQ1VSTDJmWU9kbUZ5em4= |
| 刘瑜、龚俐、童庆禧, 2014, 《空间交互作用中的距离影响及定量分析》, 《北京大学学报(自然科学版)》第5期. http://www.doc88.com/p-0961515994203.html |
| 龙翠红, 2011, 《中国的收入差距、经济增长与教育不平等的相互影响》, 《华东师范大学学报(哲学社会科学版)》第5期. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFD2011&filename=HDSD201105022&v=MjA4MDFyQ1VSTDJmWU9SdUZpSGdWTHZCTFNuWWFyRzRIOURNcW85SFpvUjhlWDFMdXhZUzdEaDFUM3FUcldNMUY= |
| 邱兆林, 2014, 《行业垄断、异质性人力资本与行业收入差距》, 《经济与管理评论》第5期. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFD2014&filename=SDJJ201405004&v=MjU0MzZWYnJPTmluQlpMRzRIOVhNcW85RllJUjhlWDFMdXhZUzdEaDFUM3FUcldNMUZyQ1VSTDJmWU9kbUZ5em4= |
| 万广华, 2009, 《不平等的度量与分解》, 《经济学(季刊)》第1期. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFD2009&filename=JJXU200901020&v=MTE0NzZaSVI4ZVgxTHV4WVM3RGgxVDNxVHJXTTFGckNVUkwyZllPZG1GeXpuV3I3UEx5ZlRlN0c0SHRqTXJvOUg= |
| 王敬勇, 2013, 《行业收入差距的原因: 垄断与人力资本孰是孰非?还是兼而有之?》, 《当代经济科学》第1期. |
| 王涛, 2014, 《基于省际面板数据的行业收入差距与经济增长关系研究》, 《统计与信息论坛》第1期. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFD2014&filename=TJLT201401011&v=Mjk3NzQ5RVpZUjhlWDFMdXhZUzdEaDFUM3FUcldNMUZyQ1VSTDJmWU9kbUZ5em5XcnpJTVNmSGVyRzRIOVhNcm8= |
| 王雪辉、谷国锋、王建康, 2016, 《产业集聚、空间溢出效应与地区工资差距——基于285个地级市的面板数据》, 《云南财经大学学报》第4期. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFDLAST2016&filename=YNCM201604006&v=MTUwNDlPZG1GeXpuV3IzTlBDUElZN0c0SDlmTXE0OUZZb1I4ZVgxTHV4WVM3RGgxVDNxVHJXTTFGckNVUkwyZlk= |
| 吴晓怡、邵军, 2016, 《经济集聚与制造业工资不平等: 基于历史工具变量的研究》, 《世界经济》第4期. http://manu30.magtech.com.cn/sjjj/CN/abstract/abstract77.shtml |
| 宗振利、武鹏, 2013, 《基于行业视角的收入差距倒U假说检验》, 《中国社会科学院研究生院学报》第3期. http://www.cqvip.com/QK/97002X/201303/45982554.html |
| 张龙、葛晶, 2015, 《人力资本、行业特征与行业收入差距——基于中国家庭追踪调查数据的研究》, 《山西财经大学学报》第11期. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFDLAST2015&filename=SXCJ201511006&v=MzA4Njg3RGgxVDNxVHJXTTFGckNVUkwyZllPZG1GeXpuVzc3T05qWElaTEc0SDlUTnJvOUZZb1I4ZVgxTHV4WVM= |
| 张世银、龙莹, 2010, 《我国收入差距扩大的影响因素及其实证分析——以行业收入变动为视角》, 《经济经纬》第4期. http://www.cqvip.com/QK/96448A/201004/34698087.html |
| 张文武、梁琦, 2011, 《劳动地理集中、产业空间与地区收入差距》, 《经济学(季刊)》第2期. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-BDGF201101001015.htm |
| 张原、陈建奇, 2008, 《人力资本还是行业特征: 中国行业间工资回报差异的成因分析》, 《世界经济》第5期. http://www.cqvip.com/QK/92713X/200805/27298708.html |
| Arbache, Jorge Saba, 2001, "Wage Differentials in Brazil: Theory and Evidence", Journal of Development Studies, Vol.38, No.2. |
| Becker, Gary S., 1975, Human Capital: A Theoretical and Empirical Analysis, with Special Reference to Education, 2nd.ed, New York: National Bureau of Economic Research. |
| Bernard Fingleton, 2006, "Beyond Neoclassical Orthodoxy: A View Based on the New Economic Geography and UK Regional Wage Data", Regional Science, Vol.84, No.3. http://strathprints.strath.ac.uk/7202/ |
| Dickens W.T. and Katz L F., 1987, Inter-industry Wage Differences and Theories of Wage Determination, Social Science Electronic Publishing. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=227501&rec=1&srcabs=242122&alg=7&pos=3 |
| Harris, C., 1954, "The Market as a Factor in the Localization of Industry in the United States", Annals of the Association of American Geographers, Vol.44, No.4. |
| Knight J.B. and R.H.Sabot, 1983, "Educational Expansion and the Kuznets Effect", American Economics Review, Vol.73, No.5. |
| Krugeger, Alan and Lawrence Summers, 1988, "Eficiency Wage and Inter-Industry Wage Structure", Econometrica, Vol.56, No.2. |
| Kuznets, 1955, "Economic Growth and Income Inequality", American Economic Review, Vol.45, No.1. http://en.journals.sid.ir/ViewPaper.aspx?ID=149496 |
| Martins P.S., 2004, "Industry Wage Premia: Evidence from the Wage Distribution", Econometrics Letters, Vol.83, No.2. |
| Mincer J., 1974, Schooling, Experience and Earnings, New York: National Bureau of Economic Research. |
| Nickell S., 1999, "Product Markets and Labour Markets", Labour Economics, Vol.6, No.1. https://dialnet.unirioja.es/servlet/articulo?codigo=300860 |
| Richard B.Freeman and Jamas Medoff, 1984, What Do Unions Do? New York: Basic Books. |
| Schettkat, Ronald, 1993, "Compensating Differentials? Wage Differentials and Empolyment Stability in the U.S. and German Economics", Journal of Economic Issure, Vol.27, No.1. |
| Thaler R.H., 1989, "Interindustry Wage Differentials", Journal of Economic Perspectives, Vol.3, No.2. https://ideas.repec.org/a/aea/jecper/v3y1989i2p181-93.html |
| Theodore W.Schultz, 1960, "Capital Formation by Education", Journal of Political Economy, Vol.68, No.6. |


