2008年全球金融危机爆发前,国际银行业监管组织主要依据资产、负债等业务的规模对系统重要性银行进行划分,其监管也往往更倾向于针对大银行。因此,学术界和监管层更关心“大而不能倒(Too Big To Fail,TBTF)”的金融机构的风险状况。
然而,在2007年10月次贷危机的初始阶段,一些资产规模并不大的金融机构如贝尔斯登、美林证券、雷曼兄弟的财务困境却引发了全球性的金融风暴,并给其他金融机构和金融体系造成了巨大损失。次贷危机及其后发生的金融危机颠覆了学术界和监管层对银行风险溢出及系统重要性的认识,“太关联而不能倒(Too Systematic To Fail,TSTF)”的机构重要性越来越受到人们的重视。在2009年4月G20伦敦峰会上,各国达成决议并设立了“全球央行”——金融稳定委员会(Financial Stability Board,FSB)。FSB、巴塞尔银行监督委员会(Basel Committee on Banking Supervision,BCBS)和国际货币基金组织(International Monetary Fund,IMF)根据“TSTF”这一理念对系统重要性金融机构的监管框架和评估方法做了修订。2011年11月,BCBS发布了《全球系统重要性银行:评估方法与附加资本吸收要求》。该要求从规模、关联性、可替代性、复杂性和跨境业务五个方面提出了全球系统重要性银行(Global-Systemically Important Banks,G-SIBs)的概念。根据上述五个方面的指标计算,FSB于2011年11月4日首次公布了29家重要性机构,我国中国银行位列其中。
BCBS发布要求后,我国银监会于2011年底发布了《关于国内系统重要性银行的划分标准征求意见稿》,将除跨境业务外的四个指标作为我国国内系统重要性银行的评估指标,并分别赋予25%的权重。
本文在Adrian和Brunnermeier(2011)的文献基础上适当改进了模型,使用条件在险值(CoVaR)模型实证研究了商业银行的系统性风险及系统重要性排名的问题。在模型处理上,本文进行了如下三个方面的改进:首先,用时变的GARCH模型对市场收益率的波动率进行处理,以克服该类研究中数据时间截点短、无法精确反映市场收益率波动的问题。其次,本文用较多的篇幅去描述并刻画我国商业银行的条件在险值、风险溢出及系统重要性程度的变化,结果更加丰富多样。最后,本文不仅从市场法的角度给出了系统重要性银行排名,还将其与目前国际和国内通行的指标法排名进行了对比和分析,结果发现依据CoVaR对银行系统重要性进行排名不仅能得出指标法的结论,还能反映那些业务结构变化明显、同业市场活跃的股份制银行在银行系统中的重要性。
二 文献回顾全球金融危机后国内外学者对系统性风险和系统重要性这两个问题展开了大量的理论和实证研究。在衡量系统重要性方面,学者们构造了许多指标,并可分为两大类(周强等,2014):(1) 指标法。主要从BCBS或银监会的有关文件和意见稿中提取相关指标的计算方法(郭卫东,2013b),或在此基础之上略作修改(巴曙松等,2012)来建立指标模型,从而对银行的系统重要性进行研究。该方法主要采用银行财务数据,从微观层面进行分析,反映的是银行过去的经营状况。(2) 市场模型法(简称“市场法”)。主要是以公开的市场股价和经济、金融数据来建立模型,由于计算过程采用了股票市场的交易数据,因此该方法能更好地反映未来不可观测到的信息。目前,国内外学者基于市场法发展了大量可以度量银行(银行体系)危机造成的系统性(单个银行)损失以及银行系统重要性的指标。其中,代表性的指标如Acharya等(2017)的边际期望损失法(MES)、Banulescu等(2015)的成分期望损失法(CES)和Brownlees等(2016)的SRISK方法。在上述指标基础上,Weiβ等(2014b)采用MES作为银行系统性风险度量指标研究了银行合并对系统性风险的影响,发现银行业的整合会使得银行业的集中程度增加,竞争程度降低,银行系统性风险上升,从而验证了“集中—脆弱”假说。Weiβ等(2014a)进一步对增加系统性风险的因素进行了实证研究,发现银行财务指标如规模、杠杆、非利息收入和信贷质量对银行系统性风险都没有持续的影响,而各国的一些宏观经济变量和管制差异反而会显著影响系统性风险的大小。范小云等(2011)应用MES指标考察了我国金融机构在美国次贷危机期间及前后对金融系统的边际风险贡献程度,发现边际风险贡献与杠杆率较高的金融机构在危机中的边际风险贡献较大,且该效应存在周期性特征。朱波等(2016)采用CES对我国2008—2014年14家上市银行系统性风险进行度量,并考察非利息收入与系统性风险的关系,发现非利息业务对大银行而言分散了系统性风险,对小银行反而加大了系统性风险,并认为信息披露质量的差异是这种非对称效应存在的原因。
近年来,随着分位数回归技术的发展,Adrian和Brunnermeier(2011)提出了条件在险值(CoVaR)的方法。该指标衡量了单个金融机构处于危机时,整个金融体系的在险值(VaR)。金融机构分别处于危机和正常状态下的条件在险值的差额(ΔCoVaR)就构成了该机构对系统性风险的贡献。同时,利用该方法中的回归系数Beta值也可以获得单个银行系统重要性的估计值。该方法提出后,Girardi等(2013)、Calluzzo等(2015)和郭卫东(2013a)据此进行了实证研究。Girardi等(2013)利用该方法得出了与Adrian和Brunnermeier(2011)不一样的结论,个体的VaR与ΔCoVaR之间无论是横截面上还是时间序列上均存在很弱的相关关系。由于Girardi等(2013)并没有完全按照Adrian和Brunnermeier(2011)的方法来定义突发事件,因此结论的不同很可能是由于指标的差异所造成的。Calluzzo等(2015)用CRSP的数据研究了2005—2011年金融机构风险的变化,发现金融危机后金融机构的个体风险变小,但是金融市场变得更加脆弱和紧密。
在因素分析上,López-Espinosa等(2012)采用全球的样本发现,银行间市场上的短期批发融资(short-term wholesale funding)是诱发系统性风险的重要原因。高国华、潘英丽(2011)分析我国14家上市银行2002—2010年的数据后发现,银行的溢出风险ΔCoVaR、自身风险VaR、不良贷款率以及宏观经济的波动均对预测银行系统性风险的边际贡献具有显著作用。
国内其他学者,如严兵等(2013)采用多变量极值模型(EVT)、范小云等(2012)采用网络分析模型、巴曙松等(2012)采用自建指数的方法、梁琪等(2013)采用SRISK方法、梁琪等(2014)采用Shapley值的方法都对银行系统重要性进行了类似研究,发现系统重要性与银行资产规模排名较为一致。
纵观现有国内外文献,全球金融危机爆发后,尤其BCBS(2011)发布系统重要性银行名单后,人们对银行系统性风险、系统重要性的研究越发重视。学者们从不同的角度构建了大量的研究指标来对各国银行体系的系统性风险和各银行的系统重要性进行了广泛而又深入的研究。各研究方法都有各自的理论假设前提和设定方法,指标在对数据拟合上也各有优劣。然而,与使用银行财务数据相比,应用股票收益率来计算系统性风险的大小较为普遍,主要因为其具有如下三方面的优势:第一,银行财务数据反映的是过去经营情况,而股价收益率具有前瞻性,反映的是市场对未来累积收益的预期;第二,按照现代资产定价的观点,股票价格是标的为公司资产的看涨期权的价格(Merton,1974),其本身就包含了公司违约的信息;第三,与基本面数据不同,股价数据具有简单、稳健、高频的特点,因此运用该数据构造有关指标来计算系统性风险能克服数据的诸多局限性(陈忠阳、刘志洋,2013)。
三 研究设计 (一) 银行的系统性风险溢出与系统重要性指标构造1.银行的条件在险值(CoVaR)。现代金融中介理论对银行市场风险的研究多使用“在险值(Value at Risk,VaR)”的方法。VaR表示在一定概率水平(q)下,银行资产或投资组合在未来某一时间内的最大可能损失。若Rti为银行i的总资产市值收益率,则银行的VaR可表示为:
| $VaR_{q}^{i}=\text{inf}\left\{ R_{t}^{i}|f\left( R\le R_{t}^{i} \right)>q \right\}$ | (1) |
本文参考Adrian和Brunnermeier(2011)以及Brunnermeier等(2012)的方法来对CoVaR进行设定:
| $\text{Probability}\left( {{R}^{system}}\le CoVaR_{q}^{system|i}|{{R}^{i}}=VaR_{q}^{i} \right)=q$ | (2) |
上式中CoVaRqsystem|i表示当银行i发生(q分位数)损失时,整个银行系统发生的最大损失(q分位数),即“银行i的条件在险值(CoVaR)”。
2.银行的系统性风险溢出(ΔCoVaR)。同理,CoVaRqsystem|medium表示银行i处于正常状态时(中位数水平)的条件在险值,定义如下:
| $\text{Probability}\left( {{R}^{system}}\le CoVaR_{q}^{system|i,medium}|{{R}^{i}}=media{{n}^{i}} \right)=q$ | (3) |
那么,CoVaRqsystem|i与CoVaRqsystem|medium的差ΔCoVaRqi就表示当单个银行发生损失时,其对系统性风险的影响。为了估计单个银行对系统性风险的贡献ΔCoVaRqi,通常需要对每家银行分别计算损失时(q分位数)和正常状态时的条件在险值(CoVaR)。首先,对银行i进行q分位数水平的分位数回归:
| $R_{t}^{i}={{\alpha }^{i}}+{{\gamma }^{i}}X_{t-1}^{i}+{{\varepsilon }^{i}}$ | (4) |
| $R_{t}^{system}={{\alpha }^{system|i}}+{{\beta }^{system|i}}R_{t}^{i}+{{\gamma }^{system|i}}X_{t-1}^{i}+{{\varepsilon }^{system|i}}$ | (5) |
其中Rti为银行i的周总资产市值收益率,Rtsystem为银行体系的总资产市值加权收益率。Xt-1i为滞后1期的状态变量,包含市场收益率、市场收益率的波动率、流动性风险、期限利差、房地产市场收益率和CPI这六个变量,具体定义如表 1所示。然后对式(4) 进行中位数水平的分位数回归:
| 表 1 主要变量定义 |
| $R_{t}^{i}={{\alpha }^{i,medium}}+{{\gamma }^{i,medium}}X_{t-1}^{i}+{{\varepsilon }^{i,medium}}$ | (6) |
利用式(4) 和式(6) 估计出来的系数,估计每家银行的VaR和中位数水平的资产收益率。
| $VaR_{q,t}^{i}=\hat{R}_{q,t}^{i}\hat{\alpha }_{q}^{i}+\hat{\gamma }_{q}^{i}X_{t-1}^{i}$ | (7) |
| $\hat{R}_{medium,t}^{i}=\alpha _{\widehat{medium}}^{i}+\gamma _{\widehat{medium}}^{i}X_{t-1}^{i}$ | (8) |
将式(7) 和式(8) 计算出的
| $CoVaR_{t}^{system|i}={{{\hat{\alpha }}}^{system|i}}+{{{\hat{\beta }}}^{system|i}}VaR_{q,t}^{i}+{{{\hat{\gamma }}}^{system|i}}X_{t-1}^{i}$ | (9) |
| $CoVaR_{t}^{system|i,medium}={{{\hat{\alpha }}}^{system|i}}+{{{\hat{\beta }}}^{system|i}}R_{medium,t}^{i}+{{{\hat{\gamma }}}^{system|i}}X_{t-1}^{i}$ | (10) |
当银行i处于不利事件并发生损失时,其对系统性风险溢出的影响如下:
| $\Delta CoVaR_{q}^{i}=CoVaR_{t}^{system|i}-CoVaR_{t}^{system|i,medium}={{{\hat{\beta }}}^{system|i}}\\ (VaR_{q,t}^{i}-R_{medium,t}^{i})$ | (11) |
3.银行的系统重要性(
结合我国上市银行的数据特征,系统性风险与系统重要性的估计中所用的各变量定义及其计算方法如表 1所示。
四 实证结果及分析 (一) 数据来源与描述性统计本文研究对象为中国16家A股上市银行,其中银行周收盘价(除权除息后)、总股本和沪深300指数数据来自Wind时间序列数据,银行杠杆率数据来自CSMAR股票交易数据库;3个月固定利率国债、3个月中证国债到期收益率和3个月Shibor数据来自Wind宏观经济数据库;房地产市场收益率采用的房地产开发综合景气指数和CPI数据来自国家统计局网站。表 2为相关变量的描述性统计。
| 表 2 变量的描述性统计 |
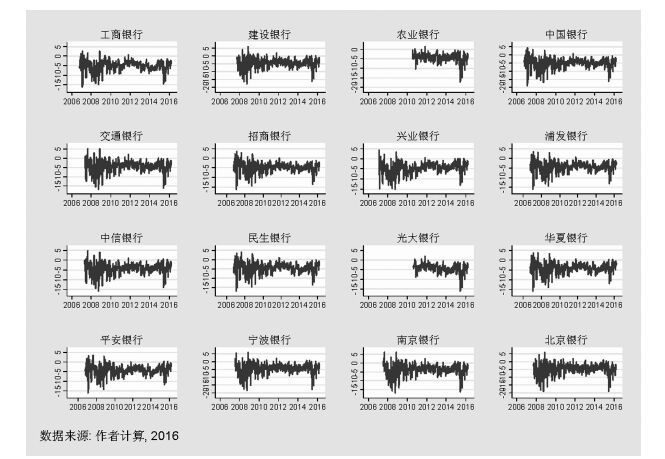
图 1给出了我国16家上市银行在5%置信水平下条件在险值(CoVaR)的动态变化,从中可以看出:我国16家上市银行中,虽然各银行的条件在险值水平大小不一,但是其变化趋势呈现出共同的特征,这说明随着我国银行业务往来的频繁,银行间联系程度的增加,我国商业银行系统中各银行在发生损失时对系统的影响会很快扩散到其他银行。
|
图 1 中国16家上市银行CoVaR的动态估计 |
表 3给出了16家上市银行CoVaR的描述性统计,从中可以看出:工商银行、中国银行、招商银行等资产规模较大、业务种类多样的银行其条件在险值的绝对值要远高于一些资产规模较小、业务种类较为单一的银行,如光大银行、平安银行、中信银行、华夏银行和南京银行。同时,对于规模较小的股份制银行,如南京银行和宁波银行,虽然其条件在险值的均值较低,但是其方差水平要高于其他银行。这说明,当损失发生时,它们尽管对银行体系造成的损失绝对值水平较低,但是会导致我国银行系统损失的频繁波动。
| 表 3 16家上市银行条件在险值(CoVaR)的描述性统计 |
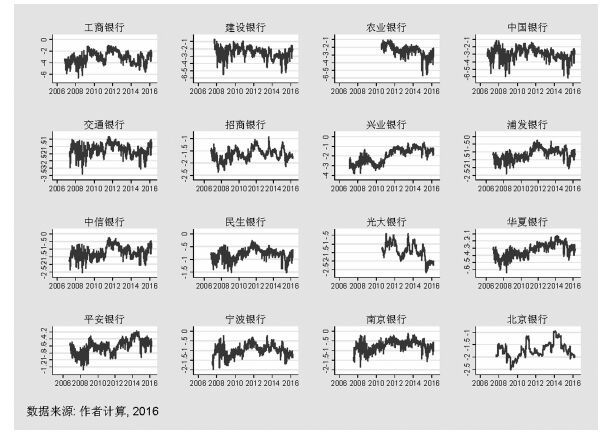
图 2给出了我国16家上市银行系统性风险溢出的估计值,与图 1不同的是,国有大型银行和股份制银行的ΔCoVaR估计值动态变化呈现不同趋势。
|
图 2 中国16家上市银行ΔCoVaR的动态估计 |
表 4给出了16家上市银行系统性风险溢出(ΔCoVaR)的描述性统计,从中可以发现该排名与经验判断基本一致,即我国传统意义上的大型国有商业银行(工商银行、建设银行、中国银行、农业银行)发生损失时,对系统造成损失的能力要远高于资产规模较小的股份制银行如宁波银行、南京银行等。同时,从历史数据来看,浦发银行虽然平均意义上对系统造成损失的能力不及招商银行、中信银行,但其ΔCoVaR的最小值和波动率要远高于上述两家银行,说明浦发银行可能是造成我国银行体系频繁发生损失的潜在来源之一。
| 表 4 16家上市银行系统性风险溢出(ΔCoVaR)的描述性统计 |
表 5给出了16家上市银行系统重要性(
| 表 5 16家上市银行系统重要性排名 |
考虑到不同的系统重要性分析方法可能会产生不同的结果,本文借鉴了巴曙松等(2012)、郭卫东(2013b)的方法对巴塞尔委员会提出的系统重要性银行指标(G-SIBs)进行了修订,构建了如表 6的分析框架,并对我国16家上市银行重新进行排名。从指标法计算的银行系统重要性排名结果看(见表 7),它与上文基于系统性风险溢出计算的结果基本一致。
| 表 6 系统重要性计算方法 |
| 表 7 指标法计算的16家上市银行系统重要性排名的动态变化 |
指标法的计算公式为:
| $\begin{align} & Scor{{e}_{it}}=规模+关联性+可替代性+复杂性 \\ & \quad =\frac{Asse{{t}_{it}}}{\sum\limits_{i}{Asse{{t}_{it}}}}+\frac{1}{3}\left( \frac{LA{{B}_{it}}}{\sum\limits_{i}{LA{{B}_{it}}}}+\frac{D{{B}_{it}}}{\sum\limits_{i}{D{{B}_{it}}}}+\frac{RC{{C}_{it}}}{\sum\limits_{i}{RC{{C}_{it}}}} \right) \\ & \quad +\frac{1}{3}\left( \frac{CC{{L}_{it}}}{\sum\limits_{i}{CC{{L}_{it}}}}+\frac{RM{{L}_{it}}}{\sum\limits_{i}{RM{{L}_{it}}}}+\frac{CR{{L}_{it}}}{\sum\limits_{i}{CR{{L}_{it}}}} \right)+\\ & \quad \frac{1}{2}\left( \frac{AS{{S}_{it}}}{\sum\limits_{i}{AS{{S}_{it}}}}+\frac{HM{{S}_{it}}}{\sum\limits_{i}{HM{{S}_{it}}}} \right) \\ \end{align}$ |
目前,国内外银行监管当局均采用的是巴塞尔委员会推出的鉴定全球系统重要性银行(G-SIBs)的方法,分别从规模、关联性、可替代性、复杂性和跨境业务五个维度来识别银行系统重要性程度。我国银行除工、建、中、农外,其他银行由于国际化程度相对较低,故未入选G-SIBs序列。银监会在判定国内系统重要性银行(D-SIBs)时也仅仅从规模、关联性、可替代性、复杂性这四个维度出发来进行测算。
表 8和表 9分别给出了我国银行系统性风险溢出(△CoVaR)和银行系统重要性程度与指标法各影响因素的实证分析。回归分析中,四个解释变量分别为采用指标法计算银行系统重要性得分时的各维度分值。根据混合效应与个体截面效应的F检验结果,本文分别呈现了最小二乘估计(OLS)、标准化各变量后的系数估计(Standard OLS)和受约束的标准化最小二乘估计(Constraint OLS)的结果。从实证结果看:第一,三种模型均显示规模与关联性的系数显著为正,可替代性与复杂性的系数在大部分实证结果中并不显著。这与我国商业银行样本期内注重外延式发展而忽略内涵式建设,同业业务发展较快,总风险敞口增加,而可替代性和复杂性相关业务发展相对较慢有很大关系。第二,标准化后的估计结果中,系统性风险溢出程度的规模因素系数(0.983) 约为关联性因素系数(0.206) 的4.8倍,带约束的标准化最小二乘估计结果与无约束估计结果相同;系统重要性规模因素系数(1.623) 约为关联性因素系数(0.224) 的7.2倍。以上结论说明:(1) 区别于巴塞尔委员会全球系统重要性银行的风险溢出,我国商业银行中规模与关联性得分越高的银行,其系统性风险溢出程度越大,银行系统重要性也越高。而可替代性、复杂性得分高低对银行系统性风险溢出程度影响并不明显。(2) 从量化结果来看,当前我国商业银行体系下,规模效应对银行系统性风险溢出的影响约为关联性效应的4.8倍,规模效应对银行系统重要性的影响约为关联性效应的7.2倍。
| 表 8 我国银行系统性风险溢出(ΔCoVaR)的影响因素 |
|
表 9 我国银行系统重要性( |
上述结论对认识我国商业银行系统性风险溢出、银行系统重要性及银行监管具有重要启示。首先,从数据结果来看,规模仍然是反映我国商业银行系统性风险溢出和银行系统重要性的主要因素,监管当局将其作为识别和监管的四因素中的首要因素具有很强的合理性。其次,随着我国银行间同业市场的发展,金融机构互持资产、互持负债以及批发融资规模的急剧增加,使得银行之间的相互关联性逐日增强,并成为影响银行系统性风险溢出的第二大因素。中国银行业也存在国际银行业普遍提及的“太关联而不能倒”的现象。最后,与银行规模和关联性因素相比,虽然近年来我国银行业托管资产、通过支付系统清算和结算的支付额、银行境外资产、业务数量、机构数量在不断增加,但是还不足以成为主导我国银行系统性风险溢出的重要因素。因此,综上所述,对我国商业银行的监管还是要将主要精力放在规模和关联性较强的银行上。
六 结论与政策建议本文采用中国16家A股上市银行2005年4月22日至2016年5月10日的收盘价数据,利用Adrian和Brunnermeier(2011)的方法对其条件在险值(CoVaR)、系统性风险溢出(ΔCoVaR)以及系统重要性(
本文的研究结论对银行经营管理层和监管部门全面认识并了解我国商业银行个体风险、系统性风险以及各银行的重要性程度提供了很重要的参考,具体来说:
第一,随着商业银行综合化经营的逐步推进,银行的业务经营范围愈加广泛。商业银行之间、银行与其他金融机构(如证券、信托、保险等)之间的联系在不断增强,这要求监管部门应将过去的只关注银行业务规模的“太大而不能倒”的理念,逐步转变为既考虑规模又强调联系的“太关联而不能倒”的理念,以适应形势发展的需要。
第二,防范我国系统性银行危机的发生,应该从系统重要性银行入手,着重加强对系统重要性银行的监管,“抓大放小”。这样既有利于降低监管成本,又能保证监管部门在危机发生的第一时间快速做出反应,提高监管效率,提升我国银行体系防范危机的能力。
第三,当前全球系统重要性银行(G-SIBs)的排名办法主要是基于发达国家的商业银行体系构造而成的,除考虑资产规模外,银行的关联性、可替代性、复杂性、跨境业务均成为某一商业银行是否能成为全球系统重要性银行的基本依据。按此测算方法,我国目前仅有工、农、中、建等国有大型商业银行位列其中。我国虽然制定了中国版的系统重要性银行(D-SIBs)测算办法,但仍基本沿用BCBS发布的测算框架和等值权重。本文研究认为,结合新型加转轨特征,监管部门应当充分考虑中国目前银行间市场尚不发达、股份制银行和城市商业银行国际化程度不高的现状,动态调整各指标权重,以更有利于对我国系统重要性银行的识别与监管。
| 巴曙松、高江健, 2012, 《基于指标法评估中国系统重要性银行》, 《财经问题研究》第9期. http://www.cnki.com.cn/Article/CJFDTOTAL-CJWT201209008.htm |
| 陈忠阳、刘志洋, 2013, 《国有大型商业银行系统性风险贡献度真的高吗——来自中国上市商业银行股票收益率的证据》, 《财贸经济》第9期. http://www.cnki.com.cn/Article/CJFDTOTAL-CMJJ201309006.htm |
| 范小云、王道平、方意, 2011, 《我国金融机构的系统性风险贡献测度与监管——基于边际风险贡献与杠杆率的研究》, 《南开经济研究》第4期. http://www.cnki.com.cn/Article/CJFDTOTAL-NKJJ201104002.htm |
| 范小云、王道平、刘澜飚, 2012, 《规模、关联性与中国系统重要性银行的衡量》, 《金融研究》第11期. http://www.cnki.com.cn/Article/CJFDTOTAL-JRYJ201211004.htm |
| 高国华、潘英丽, 2011, 《银行系统性风险度量——基于动态CoVaR方法的分析》, 《上海交通大学学报(自然科学版)》第12期. http://www.cnki.com.cn/Article/CJFDTOTAL-SHJT201112003.htm |
| 郭卫东, 2013a, 《中国上市银行的系统性风险价值及溢出——基于CoVaR方法的实证分析》, 《北京工商大学学报(社会科学版)》第4期. http://www.cnki.com.cn/Article/CJFDTOTAL-BJSB201304014.htm |
| 郭卫东, 2013b, 《中国上市银行的系统重要性评估——基于指标法的实证分析》, 《当代经济科学》第2期. http://www.cnki.com.cn/Article/CJFDTOTAL-DJKX201302006.htm |
| 梁琪、李政, 2014, 《系统重要性、审慎工具与我国银行业监管》, 《金融研究》第8期. http://www.cnki.com.cn/Article/CJFDTOTAL-JRYJ201408003.htm |
| 梁琪、李政、郝项超, 2013, 《我国系统重要性金融机构的识别与监管——基于系统性风险指数SRISK方法的分析》, 《金融研究》第9期. http://www.cnki.com.cn/Article/CJFDTOTAL-JRYJ201309005.htm |
| 严兵、张禹、王振磊, 2013, 《中国系统重要性银行评估——基于14家上市银行数据的研究》, 《国际金融研究》第2期. http://www.cnki.com.cn/Article/CJFDTOTAL-GJJR201302006.htm |
| 周强、杨柳勇, 2014, 《论中国系统重要性银行识别——市场模型法还是指标法》, 《国际金融研究》第9期. http://www.cnki.com.cn/Article/CJFDTOTAL-GJJR201409008.htm |
| 朱波、杨文华、邓叶, 2016, 《非利息收入降低了银行的系统性风险吗?——基于规模异质的视角》, 《国际金融研究》第4期. http://www.cnki.com.cn/Article/CJFDTOTAL-GJJR201604006.htm |
| Acharya V.V., Pedersen L.H. and Philippon.T., 2017, "Measuring Systemic Risk", The Review of Financial Studies, Vol.30, No.1. |
| Adrian T. and Brunnermeier M.K., 2011, "CoVaR", NBER Working Paper, No.17454, Available at NBER:https://www.nber.org/paper/w17454. |
| Banulescu G. and Dumitrescu E., 2015, "Which are the SIFIs? A Component Expected Shortfall Approach to Systemic Risk", Journal of Banking & Finance, Vol.50. http://linkinghub.elsevier.com/retrieve/pii/S037842661400051X |
| Basel Committee on Banking Supervision(BCBS), 2011, Basel Ⅲ:A Global Regulatory Framework for More Resilient Banks and Banking Systems——Revised Version June 2011, Standards and Monitoring. http://www.hofinet.org/documents/doc.aspx?id=167 |
| Brownlees C.T. and Engle R.F., 2017, "SRISK:A Conditional Capital Shortfall Measure of Systemic Risk", The Review of Financial Studies, Vol.30, No.1. https://ideas.repec.org/p/srk/srkwps/201737.html |
| Brunnermeier M.K., Dong G.N. and Palia D., 2012, "Banks' Non-interest Income and Systemic Risk", AFA 2012 Chicago Meetings Paper, January 31, 2012, Available at SSRN:https://ssrn.com/abstract=1786738. http://dx.doi.org/10.2139/ssrn.1786738 |
| Calluzzo P. and Dong G.N., 2015, "Has the Financial System Become Safer after the Crisis? The Changing Nature of Financial Institution Risk", Journal of Banking & Finance, Vol.53. |
| Girardi G.and Ergün A.T., 2013, "Systemic Risk Measurement:Multivariate GARCH Estimation of CoVaR", Journal of Banking & Finance, Vol.37. http://dx.doi.org/10.2139/ssrn.1783958 |
| López-Espinosa G., Moreno A., Rubia A. and Valderrama L., 2012, "Short-term Wholesale Funding and Systemic Risk:A Global CoVaR Approach", Journal of Banking & Finance, Vol.36. http://linkinghub.elsevier.com/retrieve/pii/S0378426612001185 |
| Merton R.C., 1974, "On The Pricing of Corporate Debt:The Risk Structure of Interest Rates", Journal of Finance, Vol.29, No.2. https://www.mendeley.com/research-papers/pricing-corporate-debt-risk-structure-interest-rates/ |
| Weiβ N.F., Bostandzic D. and Neumann S., 2014a, "What Factors Drive Systemic Risk During International Financial Crises?" Journal of Banking & Finance, Vol.41. http://linkinghub.elsevier.com/retrieve/pii/S0378426614000090 |
| Weiβ N.F., Neumann S. and Bostandzic D., 2014b, "Systemic Risk and Bank Consolidation:International Evidence", Journal of Banking & Finance, Vol.40. http://linkinghub.elsevier.com/retrieve/pii/S0378426613004536 |


