经济资本是现代保险企业重要的风险管理工具(Matthew Clark & Chris Olechowski,2008)。经济资本(Economic Capital)的概念由2004年6月25日公布的“新巴塞尔协议”正式提出。事实上,经济资本的管理思想早在上世纪90年代末就在西方先进金融企业中初现端倪。在实践中,有几个重要类型的资本要求,包括监管资本、评级机构资本以及经济资本。与监管者要求的最低资本或评级机构要求的资本水平不同,经济资本的计算一般指公司从自身业务角度出发进行资本管理。目前尚无关于经济资本的统一定义,本文将经济资本定义为对付非预期风险而应持有的资本。
国外经典文献主要集中研究风险的度量方法与经济资本测算。例如,一致性风险度量与资本测算(Artzner et al, 1999)、Value-at-Risk度量与资本测算(Jorion, 2000)、TVaR风险度量与资本测算(Overbeck, 2000)等等。因为研究问题的侧重点不一样,经典文献往往使用简单的风险相依假设,如风险独立性假设或线性相关假设。然而,现代金融产品的多样化及保险合同的复杂性使人们发现线性相关假设存在一定的局限性,如存在线性无关却正相依的风险结构(详细案例参见M.Denuit,J.Dhaene & M.Goovaerts,2006)。因此,如何整合风险成为保险公司总经济资本测算的一个关键问题。最近几年Copula理论的发展为人们整合风险提供了理论基础。
最近,相关领域的一些学者已将Copula理论应用在经济资本的测算中。Andrew Tang和Emiliano A.Valdez(2009)利用Copulas理论研究了不同Copulas相依结构下经济资本的要求及其扩散化效应。Bagarry Marc(2007)利用Student Copula函数对非寿险公司之间的相依性和经济资本的扩散化效应进行了估计。不过,国内学者在研究多风险的经济资本配置时仍然使用简单的假设,即风险的线性相关假设(陈迪红、林晓亮,2008)。通过对现有文献的整理, 我们发现国内学者至今还没有在对产品业务线经济资本配置的研究中采用Copula技术处理风险相关性。
承保风险是财险公司经营所面临的重要风险之一, 通过刻画各业务线承保风险之间的相依结构,可以较为逼真地反映各条业务线之间的相关关系及其扩散化效应,建立保险公司适度的经济资本,从而对企业的价值最大化和偿付能力充足等多目标的实现具有十分重要的意义。因此,与以往研究有所不同,本文将立足于从监管者的视角对我国整个保险行业水平上的承保业务风险进行经济资本测算,其根本目标在于为监管者制定政策提供理论和技术支持。
鉴于中国保险业处于新型市场,主要面临承保业务风险,本文着重研究基于多元Copula函数在保险企业承保业务风险经济资本测算中的应用,并对国内现有文献作出以下补充:(1)利用Student Copula和Normal Copula函数拟合我国财险企业承保业务风险之间的相依结构,并使用2000—2008我国财险市场有效数据进行拟合优度检验,实证结果表明,Student Copula对我国财险业务的相依结构拟合性较好;(2)不同风险测度下通过Student Copula相依结构测算的总经济资本普遍高于对应Normal Copula相依结构下的总经济资本;(3)与线性相依结构下的承保业务风险经济资本进行比较,Student Copula结构下的VaR或TVaR略高于后者。本文以下的结构安排是:第二部分是对Copula理论的介绍;第三部分是对经济资本计量建模;第四部分是模拟与实证研究;第五部分是结论。
二 Copula函数和尾部相关性Coupla函数实际上是一种将联合分布和它们各自的边际分布连接在一起的函数,因而也被称为连接函数。Sklar(1959)证明,任何任意随机向量Y=(Y1,Y2,…,Yn)的联合分布函数FY可以通过Copula函数表示为如下形式:
| $ \begin{array}{l} {F_y}\left({{y_1}, \cdot \cdot \cdot {\rm{, }}{y_n}} \right) = P\left({{Y_1} \le {y_1}, \cdot \cdot \cdot {\rm{, }}{Y_n} \le {y_n}} \right)\\ = C\left({P\left({{Y_1} \le {y_1}} \right), \cdot \cdot \cdot {\rm{, }}P\left({{Y_n} \le {y_n}} \right)} \right)\\ = C\left({{F_{{Y_1}}}\left({{y_1}} \right), \cdot \cdot \cdot {\rm{, }}{F_{{Y_n}}}\left({{y_n}} \right)} \right) \end{array} $ |
其中,FYi(i=1, …,n)是随机变量Yi(i=1, …,n)的边际分布函数。
当随机变量连续时,Copula函数的密度函数c可表示为:
| $ c\left({{F_{{Y_1}}}\left({{y_1}} \right), \cdot \cdot \cdot {\rm{, }}{F_{{Y_n}}}\left({{y_n}} \right)} \right) = \frac{{\partial {}^nC\left({{F_{{Y_1}}}\left({{y_1}} \right), \cdot \cdot \cdot {\rm{, }}{F_{{Y_n}}}\left({{y_n}} \right)} \right)}}{{\partial {F_{{Y_1}}}\left({{y_1}} \right), \cdot \cdot \cdot {\rm{, }}\partial {F_{{Y_n}}}\left({{y_n}} \right)}} $ |
n元变量分布函数FY的密度函数fY可表示为:
| $ {f_Y}\left({{y_1}, \cdot \cdot \cdot {\rm{, }}{y_n}} \right) = c\left({{F_{{Y_1}}}\left({{y_1}} \right), \cdot \cdot \cdot {\rm{, }}{F_{{Y_n}}}\left({{y_n}} \right)} \right)\prod\limits_{i = 1}^n {{f_{{Y_i}}}} \left({{y_i}} \right) $ |
其中,fYi(i=1, …,n)是FYi(i=1, …, n)的密度函数(参见Joe H.,1997)。
就金融保险业务而言,我们经常能观察到不同业务的极端事件同时发生(如2008年的金融危机)。尾部相关性反映了极端事件的相依结构,(上尾)尾部相关系数被定义为:
| $ \lambda = \mathop {\lim }\limits_{\alpha \to - {1^{ - 1}}} P\left({Y > F_Y^{ - 1}\left(\alpha \right)\;\;\left| {X > F_Y^{ - 1}\left(\alpha \right)} \right.} \right) $ |
其中,X、Y为任意随机变量。
两个普遍使用的多元Copula函数为多元Gaussian Copula和多元Student Copula函数。两个Copula函数的具体表达式参见Robert等(1999)。
应当注意的是,Normal Copulas具有零尾部相关性,多元Student Copula函数具有正的(上尾)尾部相关性。Normal Copula和Student Copula还有一个有趣的性质:任意一对随机向量,其线性协方差矩阵和Kendall's Tau系数之间的关系可表示为(Lindskog et al., 2003:149—156):
| $ {\rho _\tau }\left({{X_1}, {X_2}} \right) = \frac{2}{\pi }\arcsin \left(\rho \right), \sum = \left(\begin{array}{l} 1\;\;\;\;\rho \\ \rho \;\;\;1 \end{array} \right) $ |
整体风险经济资本计量是风险预测的一个部分,它是指保险公司需要考虑在一个短期或长期时间范围内的大额低概率的损失。对保险公司而言,评估多元化的活动、产品、业务所引致的经济资本,一是需要考虑所有这些产品都有着不同层次、不同程度的经济资本;二是需要考虑所有产品的风险不完全相关性,确定经济资本减少额度。这样,通过风险分类的方式,在整体基础上显示公司总的经济资本,同时考虑了由于风险不完全相关所造成的减少程度。
对单个风险的经济资本测算包含以下关键步骤:(1)评估期限为一年期;(2)风险的测度为VaR或TVaR;(3)基于基本情景下的经济资本测算。对于多个风险的经济资本测算,除以上步骤外,还需要考虑风险相关性,因而需考虑如何对风险进行整合。本文拟采用线性相依结构、正态Copula和Student Copula三种相依函数拟合各保险业务间的相依结构,并将检验各自的拟合优度和比较其结果,采用球型Copula函数拟合各类保险业务之间的相依结构主要借鉴了国外相关文献的结论,如Bagarry Marc(2007)指出,Student Copula是模拟金融业务风险相依性的较好模型。
在线性相依结构的假设下,在测算单个风险的经济资本之后,再利用平方根法则和方差—协方差矩阵,计算总的经济资本,如N类承保业务的经济资本为:
| $ {C_A} = \sqrt {\sum\limits_{i = 1}^n {C_i^2} + \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {{\rho _{ij}}{C_i}{C_j}} } } $ |
在Copula函数相依结构假设下,测算总的经济资本包括以下几个步骤:(1)各单个风险(赔付率)的边际分布的获得;(2)Copula函数的参数估计;(3)Copula函数的随机模拟;(4)Copula函数拟合优度检验;(5)基于Copulas函数的随机模拟产生的赔付率数据,测算VaR或TVaR值。
四 实证分析 (一) 数据来源本文采用了机动车辆险、企财险、货物运输险、责任保险、其他保险五个变量。其中,其他保险包括短期健康险、意外伤害保险等,主要由于2003年以前,这些业务数据的统计口径是集中统计的,后来才被分类。鉴于其他业务的市场份额较小,本文仍按以前的方式对2003年后的相关数据进行了汇总。这样,我们收集整理了1999—2008年财险市场年度相关保险业务数据。
(二) 各业务赔付率边际分布及参数估计每类业务的赔付率的边际分布是基于Copula函数进行总赔付分布拟合的基本要素。这里我们先假定每类业务的年度赔付率服从预先决定的分布。由于赔付率本身的大小表明了每类保险业务的损失严重性程度,因此,本文预设赔付率分布类型应与损失额的分布类型相似。
由于每类财险业务风险不同,每类损失额分布也会彼此不同。这就要求我们选取恰当的分布假设。由于本文的主要目的是测量经济资本,很大程度上依赖于赔付额的右尾行为,因此,理论分布的右尾行为能否恰当地与每类业务的赔付率分布相匹配将直接影响经济资本额的测算结果。根据风险理论,本文考虑两种常见的右拖尾的理论分布类型:对数正态分布和Gamma分布。其中,对数正态分布右尾偏重。
根据每类业务赔付率的直方图,我们可以对每类业务的右尾行为进行排序,由此我们初步决定各类业务的理论分布类型,如表 1所示。
根据1999—2008年的我国财险市场数据,对各类业务赔付率分布作参数估计,如表 1所示。
| 表 1 边际分布与参数估计 |
我们需要寻求最适合的Copula。Archimedean Copula常常是被选择的对象,但是它对变量之间的相依结构的复杂性不容易识别,尤其是在多变量的情形下,很难真实地模拟相依性。而Elliptical Copula函数则能处理较为复杂的多变量相依结构,事实上,多纬度参数方差—协方差矩阵允许结构形状的多样性,比Archimedean Copula参数更易理解。
Normal Copula和Student Copula是典型的Elliptical Copula。如前所述,Normal Copula具有零尾部相依性,相比之下,Student Copula更适合我们研究的问题,我们将在后面对此假设进实证检验。
根据此假设,需要进一步估计Student Copula的参数,为了比较,我们不妨同时估计Normal Copula参数。
2 方差—协方差矩阵参数R和参数v的估计对于Student Copula和Normal Copula中的协方差矩阵参数R的估计, 我们借鉴Bagarry Marc(2007)参数估计方法。方差—协方差矩阵参数R的估计结果如表 2所示。
| 表 2 方差—协方差矩阵 |
利用极大似然估计方法,Student Copulas参数的估计结果如图 1所示,算得的值为27时,对数似然函数值最大。
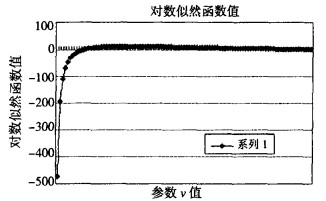
|
图 1 参数的估计 |
在对Copula函数参数估计之后,接下来我们将产生基于Normal Copula函数和Student Copula函数的每类业务赔付率的模拟数据,模拟程序借鉴Embrechts et al(2003)。
(五) Copula函数的拟合优度检验为了检验利用Normal Copula和Student Copula拟合我国财险市场业务相依结构是否合适,本文借鉴相关文献提供的三种检验方法。
第一种检验方法即通过类别之间的距离,比较模拟数据对被观察数据的拟合程度。如果我们定义第I类为区间[(i-1)/10, i/10], 我们能够估计任意一对保单(X, Y)的模拟值分别属于I类和J类的概率:即:
| $ {P_{xy}}\left({i, j} \right) = P\left({{U_x} \in I, {U_y} \in J} \right) $ |
我们根据历史数据估计Pxy的估计式为:
| $ P_{xy}^{Emprical}\left({i, j} \right) = \frac{1}{T}\sum\limits_{t = 1}^T {{1_{{\mu _{xt}}}} \in I, et, {\mu _{yt}}} \in J $ |
根据模拟数据估计Pxy的估计式为:
| $ P_{xy}^{Emprical}\left({i, j} \right) = \frac{1}{S}\sum\limits_{t = 1}^S {{1_{{r_{xt}}}} \in I, et, {r_{yt}}} \in J $ |
其中,T为历史数据数量(T=41),S为模拟数据数量(S=2000),μxt为X业务的Copula第t个历史实现值,rxt为X业务的Copula第t个模拟实现值。
我们能计算检验的Copula与经验的Copula之间的距离,即:
| $ d_{xy}^{Testedcopula} = \sum\limits_{\left( {i,j} \right)}^{} {{{\left( {P_{xy}^{Emprical}\left( {i,j} \right) - P_{xy}^{Emprical}\left( {i,j} \right)} \right)}^2}} $ |
通过该检验方法得到我国财险市场数据检验的结果,如表 3所示。
| 表 3 相依结构的检验 |
表 3表明,由Student Copula产生的数据与经验数据之间的偏差比Normal Copula下相关数据偏差要小些,这意味着Student Copula相依结构假定优于Normal Copula相依结构假定。
第二种检验方法是给定分位数,即测算球形Copula累积分布函数与经验Copula累积分布函数之间的距离来分析被观察数据与Copula相依结构下产生的模拟数据之间的拟合程度。
| $ \begin{array}{l} D\left(q \right) = {C^{El}}\left({q, q, q, \ldots q} \right) - {C^{em}}\left({q, q, q, \ldots q} \right)\\ {C^{em}}\left({q, q, q, \ldots q} \right)\frac{1}{T}\sum\limits_{t = 1}^T {{1_{{u_x}t}} \le q, \ldots {u_{yt}}} \le {q_{yt}}\\ {C^{El}}\left({q, q, q, \ldots q} \right) = \frac{1}{S}\sum\limits_{t = 1}^S {{1_{{r_x}t}} \le q, \ldots {y_{yt}}} \le {q_{yt}} \end{array} $ |
利用我国财险市场数据检验的结果,如表 4所示。
| 表 4 给定分位数下不同Copula结构下的D(q) |
表 4表明,Student Copula相依结构D(q)比Normal Copula相依结构下对应的D(q)要小些,这意味着Student Copula相依结构假定优于Normal Copula相依结构假定。
第三种检验方法的基本思想是,比较在几个业务中同时超过给定分位数的概率,记为:
| $ p\left(u \right) = p\left({{U_1} \ge u \ldots, {U_n} \ge u} \right) = C\left({1 - u, \ldots, 1 - u} \right) $ |
其估计量为:
| $ p\left(u \right) = \frac{{\sum\limits_i {{\mathit{u}_{1i}} > u, {u_{2i}} > u, \ldots, {u_{ni}} > u} }}{{i的个数}} $ |
记
| $ r\left(u \right) = \frac{{{p^{Student}}\left(u \right)}}{{{p^{Normal}}\left(u \right)}} $ |
利用我国财险市场数据检验的结果,如表 5所示。
| 表 5 Copula模拟产生的各业务赔付率同时超过给定分位数的个数 |
表 5表明,Student Copula相依结构模拟产生的各业务赔付率同时超过给定分位数的个数,多于对应Normal Copula模拟产生的各业务赔付率同时超过给定分位数的个数,这与理论上Student Copula的尾部相依程度高于Normal Copula的结论一致,也验证了Student Copula较Normal Copula刻画尾部相依结构的优越性。
(六) 整合的总赔付率 1 整合的赔付率将以上过程重复10 000次,分别得到基于Normal Copula和Student Copula相依结构的10 000个赔付率向量随机模拟实现值。利用各业务的市场份额作为权重,加总各业务赔付率,我们能得到不同相依结构下整合的总赔付率分布,这里我们提供Normal Copula和Student Copula相依结构下整合的总赔付率直方图,如图 2。
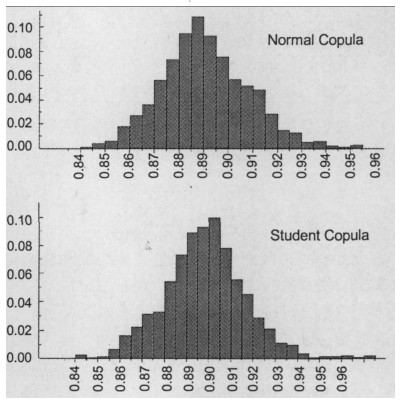
|
图 2 总赔付率直方图 |
VaR和TVaR风险测度下基于多元Copula函数相依结构下的整合的财险业务经济资本,如表 6所示。
| 表 6 整合的财险业务经济资本及尾部相依性 |
表 6显示,VaR风险测度下基于多元Copula函数相依结构的整合的财险业务经济资本普遍低于TvaR风险测度下相应的经济资本,且Student Copula相依结构下整合的经济资本普遍大于对应的Normal Copula相依结构下整合的经济资本。这是因为Student Copula考虑了更大的业务尾部相依性。
3 整合的经济资本与分散效应如果将基于多元Copula函数的相依结构和财险业务经济资本总和加以比较,我们可以得到如表 7所示的结果。
| 表 7 整合的财险业务经济资本与分散效应 |
表 7表明,财险业务经济资本总和普遍大于对应的整合的经济资本,这是由于业务风险分散产生的效应,即各业务风险的不利结果不同时发生。
(七) 与线性相依结构下承保业务风险经济资本的比较利用我国财险市场2000—2008年的承保业务有效数据,在线性相依结构的假定下,我们测算得VaR和TVaR风险测度下财险业务总经济资本,如表 8所示。
| 表 8 与线性相依结构财险业务经济资本的比较 |
表 8显示,Student Copula相依结构下整合的经济资本普遍大于对应线性结构下整合的经济资本。
五 结论本文在VaR和TVaR的风险测度下, 运用基于多元Copula函数的财险产品业务线之间相依结构的经济资本测算,同时根据《中国保险统计年鉴》中各家保险公司的数据,实证分析得到如下结论:
第一,通过拟合优度检验,运用Student Copula函数拟合我国财险市场业务的相依结构要优于运用Normal Copula函数。
第二,同一置信水平下测算得到的财险业务经济资本计量结果由高到低的顺序为:基于TVaR测度及Student Copula结构下测算的总经济资本、TVaR测度及Normal Copula结构下测算的总经济资本、VaR风险测度及Student Copula相依结构下测算的总经济资本、VaR风险测度及Normal Copula相依结构下测算的经济资本。
第三,分别比较Student Copula相依结构与线性相依结构假设下测算的承保业务风险总经济资本,发现不同相依结构假设下所测算得到的经济资本存在明显差异。
产生上述现象的可能原因有:(1)由于宏观经济和市场环境等客观因素的影响, 我国保险产品面临的系统性风险较大,从而导致财险承保业务风险尾部共同单调性较高;(2)我国财险市场产品设计中风险分散化程度不够。
正如以上结论所示,不同的相依结构假设对经济资本的计量非常敏感。我国保险业目前正在经历偿付能力资本(经济资本的监管者视角)监管的变革,但现有的偿付能力最低资本标准对各业务之间的相关性没有加以考虑。因此,一方面,本研究通过使用Copula函数对实际业务线相依结构拟合,并进行拟合优度检验,力求刻画各业务线之间的真实的相依关系,使整个建模和实证过程能够对监管者指定与保险市场实际风险相适应的最低偿付能力资本标准提供理论和技术支持; 另一方面,本文结论显示,选用Student Copula拟合我国财险市场业务的相依结构存在相对优势。
本文仅考虑了财险公司各条产品业务线承保风险的经济资本配置, 因而进一步的研究方向是,考虑投资风险如信用风险和市场风险的影响, 并顾及不同再保险策略下的经济资本测算。
陈迪红、林晓亮, 2008, 《我国财险公司产品业务线经济资本配置的实证分析》, 《财经理论与实践》第11期。 |
Artzner, P., Delbaen, F., Eber, J.M. and and, Heath D., 1999, "Coherent Measures of Risk", Mathematical Finance, No.9. |
Andrew Tang, Emiliano A.Valdez, 2009, Economic Capital and the Aggregation of Risks using Copulas,
Meeting Paper for the 28th International Congress of Actuaries. https: //papers.ssrn.com/sol3/papers.cfm?abstract_id=1347675
|
Bagarry Marc, 2007, Economic Capital : a Plea for Student Copula, Meeting Paper for the 28th International Congress of Actuaries.
|
Charpentier, A., 2008, Dynamic Dependence Ordering for Archimedean Copulas and Distorted Copulas, Kybernetika, in press.
|
Embrechts P, Lindskog F, McNeil A., 2003, "Modeling Dependence with Copulas and to Risk Management", In Rachev(ed), Handbook of Heavy Tailed Distributions in Finance, Elsevier: Amsterdam.
|
Joe, H., 1997, "Multivariate Models and Dependence Concepts", Journal of Political Economy, No.71. |
Jorion, P., 2000, Value at Risk, 2nd Edition, Academic Press: San Diego.
|
M.Denuit, J.Dhaene, M.Goovaerts, et al, 2006, Actuarial Theory for Dependent Risks Measures, Orders and Models, www.wiley.com.
|
Matthew Clark, Chris Olechowski, 2008, Economic Capital Correlations Matrices and other Techniques, www.soa.og.
|
Overbeck, L., 2000, "Allocation of Economic Capital in Loan Portfolios, " In Franke J., Haerdle W. and Stahl G. (eds), Measuring Risk in Complex Systems, Springer.
|
Robert, T.Clemen and Terence, Reill, 1999, "Correlations and Copulas for Decision and Risk Analysis", Management Science, Vol.45, No.2. |
Sklar.A., 1959, Fonction de Revpartition av nv Dimensions et Leurs Marges, Publications de l''Institut Statistique de l''Universite de Paris, 8 229-231.
|


