我国股票市场在不同时期的表现差异明显。2005年至2009年,上证综指从1012.1点(2005年7月18日)攀升至6124点(2007年10月16日),上涨近6倍,尔后暴跌至1664点(2008年10月28日)。2010年至2014年,上证综指在1900点至3200点间波动。自2015年开始,股票市场又开始了剧烈震荡。而对应时段内,通货膨胀水平也有一定的波动。2006年至2009年,CPI同比从0.80%(2006年3月31日)持续增长至8.74%(2008年2月29日),随后又持续下降至-1.81%(2009年7月31日),从通货膨胀状态陷入通货紧缩状态。2010年至2011年CPI再次攀升,从1.53%(2010年1月)攀升至6.45%,处于温和通胀的状态,随后降低至2012年10月的1.7%,之后处于较为稳定的状态。与上述过程相伴的,是投资者将闲置资金投资于房地产市场和股票市场以进行资产的保值和增值。那么,投资于股市所取得的收益是否可以对冲通货膨胀从而实现资产保值呢?这是本文研究的问题。
“费雪假说”认为名义利率能够充分地反映通货膨胀的变化。将这种关系拓展至资本市场,若“费雪假说”成立,则股票收益能够对冲通货膨胀,形成“广义的费雪效应”。然而对不同国家市场、不同时间段的实证研究得出了不同的结论,形成了“股票收益—通货膨胀之谜”。本文从区制依赖性的角度出发,使用马尔科夫区制转换模型,研究实际股票收益在不同区制下对通货膨胀做出的不同反应。
本文的研究贡献主要在于:第一,将通货膨胀划分为低通胀、温和通胀和高通胀3个区制,符合我国经济发展的特殊性,更加精确地分析了实际股票收益率与通货膨胀水平的非对称关系;第二,利用MS-VAR模型①自身及区制转换的脉冲响应函数分析了发生外部冲击及经济系统发生转换时实际股票收益率与通胀率的响应程度及路径。
二 文献综述通货膨胀率和实际股票收益率之间相关性一直是宏观经济及金融等研究领域的热点问题之一。两者关系较为复杂,不同的市场发展阶段以及对模型选择均会使检验结果产生差异。费雪(Fisher,1930)认为实际股票收益率不受物价变动的影响而保持常数,从而得出股票是优质保值产品的结论。
而在此之后的若干实证研究却得出了不同的结论。部分学者证明了当一个国家处于高通胀时,通货膨胀率和股票收益率之间呈正相关,支持“费雪效应”的论断(Gultekin,1983;Barnes, et al., 1999;Crosby,2001;薛福星,2006;赵留彦,2016)。但仍有相当数量的实证结果(Bodie,1975;Nelson,1976;Fama,1977)表明通胀率与实际股票收益率之间是负相关关系,甚至在某些情况下通胀率与名义股票收益率也呈负相关的态势,“股票收益—通货膨胀之谜”(也称为“费雪效应悖论”)由此产生。各国学者提出了不同的理论假说用来解释这一现象,Modigliani等(1979)的通货膨胀幻觉假说指出,投资者采用名义利率而非实际利率对公司的盈利进行贴现导致股票价格高估或者低估,具体表现为在高通胀时期低估股票价格,在低通胀或通货紧缩时期高估股票价格。Fama(1981)的“代理假说”认为股票收益率和通胀率之间自身不存在相关性,两者之间呈负相关是因为股票收益率和通胀率均受实体经济的影响。Kaul(1987)的“反向假说”认为股票收益率与通胀率之间的相关性由货币政策决定,如果央行的货币政策逆周期操作,两者之间的负相关性会更加显著,而如果央行顺周期操作,会弱化两者之间的负相关性甚至直接导致两者正相关。Cornell(1983)的“风险溢价假说”引入了未预期通胀的概念,当通胀率较高且远远超过预期通胀时,风险溢价增加,贴现率也会随之提高,依据现金流折现方法对上市公司进行估值时,必然会使得公司未来现金流下降,股票内在价值下跌,从而导致股价下跌。
此外,相关研究表明股票收益率与通货膨胀率之间具有不确定的关系,即存在门槛效应。Hess和Lee(1999)对二战前后不同国家的数据进行实证分析的结果表明,通胀率与股票收益率在二战前表现为显著的正相关性,而在二战后表现为负相关性。其后,Kolluri和Wahab(2008)的研究结果表明线性模型等不足以描述股票收益和通货膨胀之间的非对称关系,通胀率较低时是负相关关系,而高通胀时是正相关关系。从我国的经验数据来看,韩学红和郑妍妍(2008)提出,股票收益率和通货膨胀率的相关关系取决于通货膨胀率上升动力的来源。如果通货膨胀是由供给导致的,两者之间呈负相关的态势,而如果通货膨胀是需求驱动的,那么两者之间呈正相关的态势。刘金全和马亚男(2009)认为两者之间的关系主要取决于股票市场的状态,“费雪效应”成立于股市显著扩张的阶段,实际股票收益率与通胀率的趋势成分表现为正相关性,而当成交量明显下降、股市严重低迷时,“代理假说”成立,通货膨胀率趋势成分与实际股票收益率呈负相关的关系。苟小菊等(2009)发现股票收益率和通货膨胀率之间存在正向的协整关系,短期内两者相关性不显著;低通胀区制内两者正相关,高通胀区制内两者负相关。
在实证研究方法上,国内大多数学者习惯利用VAR、SVAR等线性模型对股票收益率与通胀率之间的关系进行实证分析(薛福星,2006;郭建军,2008;韩学红等,2008;赵留彦,2016;王宇伟等,2018),忽略了经济增长变动引起的禀赋变化、相关政策的变动、羊群效应等导致经济时间序列出现明显偏离趋势的诸多因素。①即使考虑了非对称效应,少数使用了马尔科夫区制转换模型的学者在刻画两者的关系时,大多忽略了温和通胀这一重要区制,仅仅将通胀水平划分为两个区制,即高通胀和低通胀,如此划分不符合我国实际的通货膨胀水平,也忽略了马尔科夫区制转换模型中最为重要的脉冲响应函数分析(刘金全等,2009;苟小菊等,2009)。
本文采用马尔科夫区制转换模型(MS-VAR)将通货膨胀水平分为低通胀、温和通胀和高通胀3个区制,对我国过去二十多年的实际股票收益率与通胀率之间的关系进行深入的研究,探索在各个区制内“费雪效应”是否存在,并结合马尔科夫区制转换模型(MS-VAR)脉冲响应函数研究外界突然产生冲击以及区制转换时两者的响应程度和路径。
三 模型与假设 (一) 理论模型:对实际股票收益率与通货膨胀率非对称关系的解释在说明通货膨胀率与实际股票收益率的关系时,根据传统的代理假说(Fama,1981)以及反向因果假说(Geske & Roll,1983)所构建的模型含有测量误差,本文借鉴Kolluri和Wahab(2008)的做法,引入一个适应性预期滤波以滤除测量误差。
| $ {\rm{E}}_t^*\left({\ln {f_{t + 1}}} \right) - {\rm{E}}_{t - 1}^*\left({\ln {f_t}} \right) = \beta \left({\ln {f_{t - 1}} - {\rm{E}}_{t - 1}^*\left({\ln {f_t}} \right)} \right) $ | (1) |
其中, lnft-1代表实际通货膨胀率的一阶滞后;Et*(lnft+1)代表t期建立的t+1期真实但不可观测的通货膨胀率的预期。
| $ {{\rm{E}}_t}\left({\ln {f_{t + 1}}} \right) = {\rm{E}}_t^*\left({\ln {f_{t + 1}}} \right) + {e_t} $ | (1.1) |
其中, Et(lnft+1)代表根据传统假说模型在t期建立的t+1期的通货膨胀估计值。假设我们所估计的适应性预期的模型是随机的,则可将式(1)重新表述为:
| $ {\rm{E}}_t^*\left({\ln {f_{t + 1}}} \right) = {\alpha _0} + {\alpha _1}{\rm{E}}_{t - 1}^*\left({\ln {f_t}} \right) + {\alpha _2}\left({\ln {f_{t - 1}}} \right) + {\varepsilon _t} $ | (2) |
其中,α1=(1-β)。在这个模型中,短期通货膨胀率的预期受其本身滞后和实际通货膨胀率滞后的影响。将式(1.1)带入式(2),可以得到:
| $ {{\rm{E}}_t}\left({\ln {f_{t + 1}}} \right) = {\alpha _0} + {\alpha _1}{{\rm{E}}_{t - 1}}\left({\ln {f_t}} \right) + {\alpha _2}\left({\ln {f_{t - 1}}} \right) + {\omega _t} $ | (2.1) |
其中,ωt=εt-α1et-1+et。根据适应性预期理论,α1和α2在数值上显著为正。
有了通货膨胀预期滤波后,接下来,考虑到我国经济发展的特点,我们提出一个非对称性的模型,用以分析实际股票收益率与预期通货膨胀率之间的关系:
| $ {R_{s, t}} = \alpha + {\beta _1}{D_1}{\rm{E}}_{t - 1}^*\left({\ln {f_t}} \right) + {\beta _2}{D_2}{\rm{E}}_{t - 1}^*\left({\ln {f_t}} \right) + {\beta _3}{\rm{E}}_{t - 1}^*\left({\ln {f_t}} \right) + {\mu _t} $ | (3) |
其中:
| $ \left({{D_1}, {D_2}} \right) = \left\{ {\begin{array}{*{20}{l}} {(1, 0)}&{{\rm{E}}_{t - 1}^*\left({\ln {f_t}} \right) < {{\left({\ln {f_l}} \right)}^*}}\\ {(0, 1)}&{{\rm{E}}_{t - 1}^*\left({\ln {f_t}} \right) > {{\left({\ln {f_h}} \right)}^*}}\\ {(0, 0)}&{{{\left({\ln {f_l}} \right)}^*}E_{t - 1}^*\left({\ln {f_t}} \right){{\left({\ln {f_h}} \right)}^*}} \end{array}} \right. $ |
(3) 式中,Rs, t表示实际股票收益率,D1和D2为虚拟变量,用以区分实际股票收益率与不同通胀水平的关系,(lnfl)*和(lnfh)*分别为设定的常数,当通货膨胀率高于(lnfh)*时代表高通胀,低于(lnfl)*时代表低通胀(通货紧缩),高于(lnfl)*但低于(lnfh)*时代表温和通胀。
式(3)是传统“费雪假说”的增广(非对称性)变换,Fisher(1930)认为如市场强式有效,则市场能够处理所有t-1期获得的信息,那么资产名义收益率包括资产实际收益率和预期通胀率,具体表示为:
| $ {\rm{E}}\left({{R_t}|{\Omega _{t - 1}}} \right) = {{\rm{E}}_{t - 1}}\left({{r_t}|{\Omega _{t - 1}}} \right) + {\rm{E}}_{t - 1}^*\left({\ln {f_t}|{\Omega _{t - 1}}} \right) $ | (4) |
其中,Rt代表资产名义收益率,rt代表基于前期信息集Ωt-1的资产实际收益率,E*(lnft)代表基于前期信息集Ωt-1的最佳通货膨胀预期的估计。“费雪假说”认为实体部门和货币部门是相互独立的,预期实际收益率由资本的生产力、投资者时间和风险偏好等因素决定,则预期实际收益率与预期通货膨胀率之间非相关,Fama和Schwert(1977)提出了一个不包含预期实际收益率的研究模型,并在长期以来被学术界用以研究名义或实际股票收益率和预期通货膨胀率之间的关系:
| $ {R_t} = \alpha + \beta {\rm{E}}_{t - 1}^*\left({\ln {f_t}|{\Omega _{t - 1}}} \right) + {\mu _t} $ | (4.1) |
可以看出,条件预期资产名义收益率是预期通货膨胀率的函数,若β等于1,则预期资产名义收益率和预期通货膨胀率呈现一比一的变化,而预期实际收益率保持不变,此时“费雪假说”成立。
将式(1.1)带入式(4.1)可以得到:
| $ {R_{i, t}} = \alpha + \beta {{\rm{E}}_{t - 1}}\left({\ln {f_t}} \right) + \left({{\mu _t} - \beta {\omega _{t - 1}}} \right) $ | (4.2) |
考虑到在不同预期通货膨胀水平下实际股票收益率与预期通货膨胀率的关系不同,我们对式(4.2)进行非对称性分析:
| $ {R_t} = \alpha + {\beta _1}{D_1}{{\rm{E}}_{t - 1}}\left({\ln {f_t}} \right) + {\beta _2}{D_2}{{\rm{E}}_{t - 1}}\left({\ln {f_t}} \right) + {\beta _3}{{\rm{E}}_{t - 1}}\left({\ln {f_t}} \right) + {\nu _t} $ | (5) |
其中:
| $ \left({{D_1}, {D_2}} \right) = \left\{ {\begin{array}{*{20}{l}} {(1, 0)}&{{{\rm{E}}_{t - 1}}\left({\ln {f_t}} \right) < {{\left({\ln {f_l}} \right)}^*}}\\ {(0, 1)}&{{{\rm{E}}_{t - 1}}\left({\ln {f_t}} \right) > {{\left({\ln {f_h}} \right)}^*}}\\ {(0, 0)}&{{{\left({\ln {f_l}} \right)}^*} \le {E_{t - 1}}\left({\ln {f_t}} \right) \le \left({\ln {f_h}} \right)^*} \end{array}} \right. $ |
我们可以通过式(5)估计在不同通货膨胀水平即在低通胀(通货紧缩)、温和通胀和高通胀下实际股票收益率与预期通货膨胀率之间的关系。
(二) 假设的提出在研究通货膨胀率和股票收益率的关系时,相当多的文献对不同市场进行了实证分析,而这些文献进行两者关系的分析时大多集中于某一时间段,因而可能没有注意到整个股票市场发展的特点。当然,也有一些学者在研究时加入门限,研究通货膨胀率与资产回报率的非对称关系。学者们从不同的角度设定阈值进行研究,一种角度是从股票市场或外在经济的状况设定门限(张兵,2005;Hondroyiannis & Papapetrou,2006;刘金全等,2009;Cifter,2015;Liu & Wang,2017),另一种角度是从通货膨胀率高低的角度设定门限(Kolluri & Wahab,2008;苟小菊等,2009;Boamah,2017;McMillan,2017)。
相比较而言,市场的状态更难预测,因此,本文从通货膨胀水平的角度出发研究实际股票收益率和通货膨胀水平的关系。而既有的文献在对通货膨胀水平进行划分时大多仅区分了低通胀和高通胀两个水平(Kolluri & Wahab,2008;苟小菊等,2009),考虑到股票市场是经济增长的“晴雨表”,保持适度通货膨胀有助于经济快速增长(刘金全等,2003),因此本文加入了温和通胀这一情形,将通货膨胀分为低通胀(通货紧缩)、温和通胀和高通胀,在此基础上分析实际股票收益率和通货膨胀水平的非对称关系,以检验“费雪假说”在我国不同条件下的适用性。接下来,本文选取几个典型的阶段对实际股票收益率和通货膨胀率的关系进行直观的分析,并提出假设。
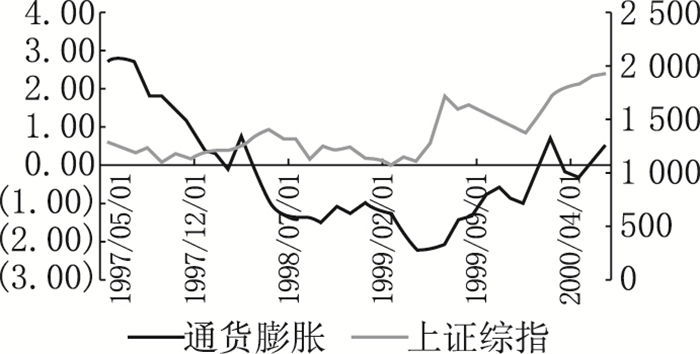
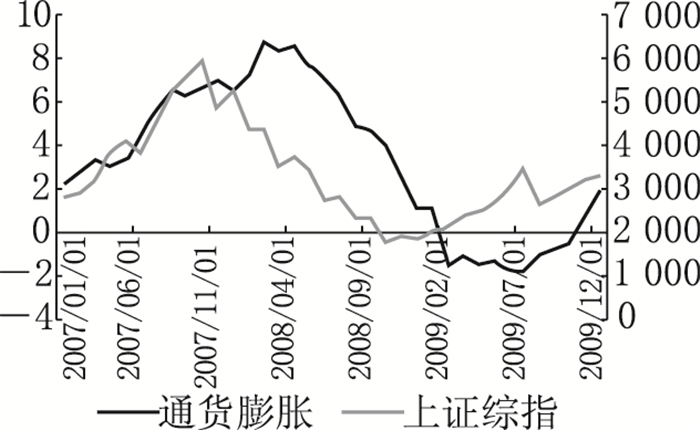
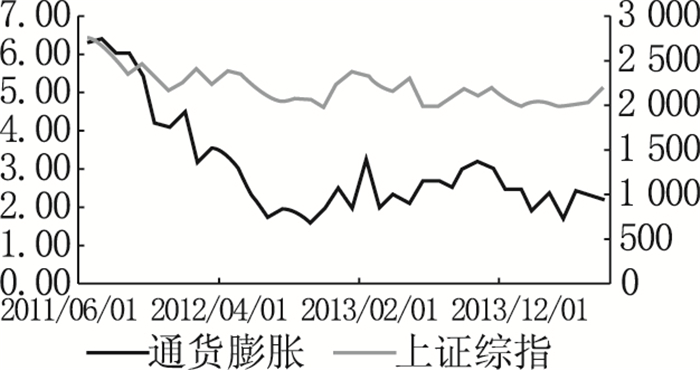
1.低通胀(通货紧缩)。我们选取了1992年以来经历的3次通货紧缩阶段,分别为1997年5月至2000年6月、2009年、2011年6月至2014年7月。由图 1可知,CPI与上证综指整体均处于低位。在这类阶段,经济加速衰退,物价持续下跌,一方面消费者对经济前景持悲观态度,投资和消费水平萎缩,另一方面,实际利率提高,增加了企业的融资成本,企业还债压力加重、投资下降,其盈利能力也下降,因此股价下跌,股市陷入低迷状态。
|
图 1a 低通胀和上证综指走势(1997—2000年) |
|
图 1b 低通胀和上证综指走势(2009年) |
|
图 1c 低通胀和上证综指走势(2011—2014年) |
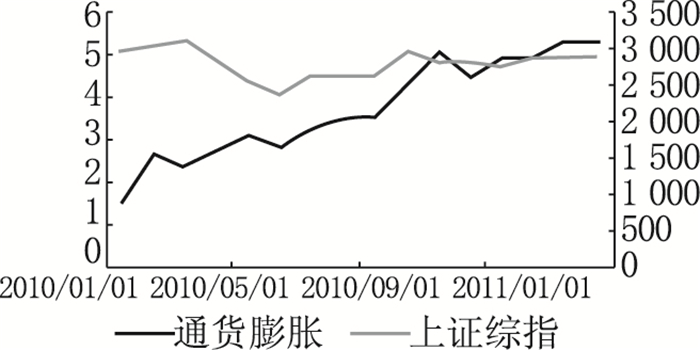
2.温和通胀。我们选取了2010年至2011年这一时期作为温和通胀阶段,在此阶段,由图 2可知,CPI有所上升但增速温和,上证综指总体向上攀升,可以看出温和通胀对股票指数有正向作用。在这段时间,一方面产品价格稳定,另一方面名义货币供应量增加使得利率下降,两者都有利于公司盈利能力的提升,从而刺激股票价格的上涨。
|
图 2 温和通胀和上证综指走势(2010—2011年) |
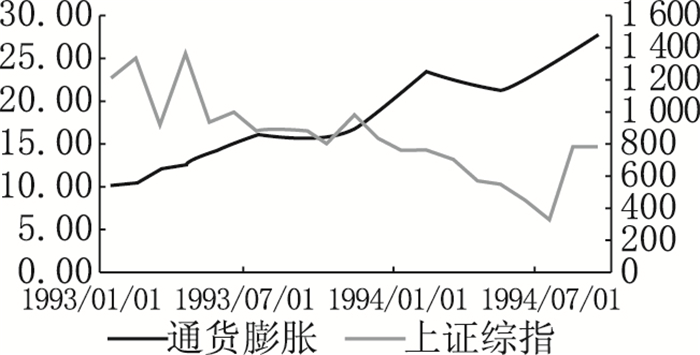
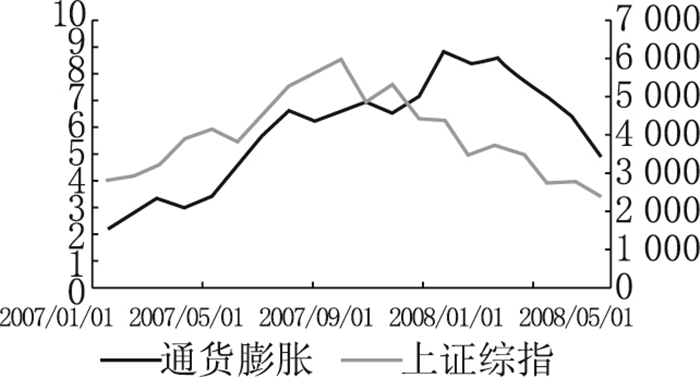
3.高通胀。1992年至1993年价格改革和2007年股权分置改革后,CPI处于高位,经济体处于严重通货膨胀状态,相对应的,1993年11月至1994年7月上证综指跌幅超过60%,2008年上证综指暴跌至1664点,因此直观看,严重通胀下,股价不断下跌,股市处于低迷的状态(见图 3)。在这类阶段,物价水平持续提高,原材料的价格随之上升,成本费用不断上涨,企业盈利能力下降,投资者基于未来公司低盈利的预期而减少投资,这加速了公司股票价格的下跌。同时,实际货币供应量下降,消费者实际购买力下降,产品供过于求,形成了恶性循环。此外,在高通胀时期,政府倾向于采取紧缩货币政策,减少货币供应量,从而使利率进一步上升,企业融资成本快速增加而使投资不足,股票市场持续低迷。
|
图 3a 高通胀和上证综指走势(1993—1994年) |
|
图 3b 高通胀和上证综指走势(2007—2008年) |
基于以上分析,本文提出如下假设:
假设一:当我国通货膨胀水平较低时,实际股票收益率偏低;
假设二:当我国处于温和通货膨胀状态时,实际股票收益率最高;
假设三:当我国处于高通货膨胀状态时,实际股票收益率最低。
四 实证分析 (一) 数据来源本文所选样本的区间为1992年1月至2016年10月。所采用的原始数据涵盖了我国证券市场发展以来经历的10次牛熊市转换①以及通胀水平的变化②,在数据可得的范围内数据长度较长,保证了结果的稳定性和严谨性,实证数据包括实际股票收益率和通货膨胀率指标。
本文实际股票收益率的指标采用上证综合指数的同比月度收益率。选择上证综合指数在于该指数覆盖面更广泛(包含A股和B股),编制相对较为合理;选择月度收益率在于我国股市波动较大,使用对数形式的收益率偏差可能更大;选择同比数据则在于我国股市仍是“政策市”,一个政策的发布容易形成一段时间内股票收益率的波动聚集效应。
本文通货膨胀率指标选择了居民消费价格指数(CPI)的同比数据。Fisher(1930)认为,若投资者投资均是为了消费,则选取CPI作为通货膨胀率的代理指标是可行的。本文数据均来源于wind数据库。
(二) 实证检验1.参数估计结果分析。本文运用Krolzig(1998)的OX-MSVAR包含的GiveWin软件,应用Hamilton(1990)极大似然方法对所建模型进行估计分析。根据信息准则确定最优滞后阶数为3,在线性VAR模型及其他4种非线性模型(MSIH(2)-VAR(3)、MSIH(3)-VAR(3)、MSIAH(2)-VAR(3)、MSIAH(3)-VAR(3))中,MSIH(3)-VAR(3)模型的拟合效果最好,最优区制数为3,与上文提出的假设划分为低通胀、温和通胀和高通胀3个区制相一致。MSIH(3)-VAR(3)模型在不同区制下的参数结果如表 1。
| 表 1 MSIH(3)-VAR(3)模型参数的估计结果 |
参数估计结果显示,截距项、自回归系数及其滞后项在不同的区制下差异较大,表明我国实际股票收益率与通胀率之间并非一直保持“正相关”或“负相关”的关系,而是随着通胀水平的变化而改变。在区制一情况下,CPI和RSH的截距分别为0.0362、-0.0473;区制二下,CPI和RSH的截距分别为0.1296、0.0249;区制三下,CPI和RSH的截距分别为1.1303、-0.7579。由此我们得出结论:状态s1表示“低通胀率(通货紧缩)和较低实际股票收益率”;状态s2表示“温和通胀和高实际股票收益率”;状态s3表示“高通胀和低实际股票收益率”。可见,参数估计结果验证了前文提出的3个假设。
从RSH方程来看,实际股票收益率的变化存在明显的“惯性”,滞后1期的实际股票收益率对当期收益率具有显著的正向影响(效应为1.0581),滞后2期和3期的收益率对当期的影响作用较弱,即前期实际股票收益率的上升会带来当期实际股票收益率的上升。滞后1期的通胀率对当期实际股票收益率具有负向作用(效应为-0.0474),表明前期通胀率的提高会导致当期实际股票收益率的降低。
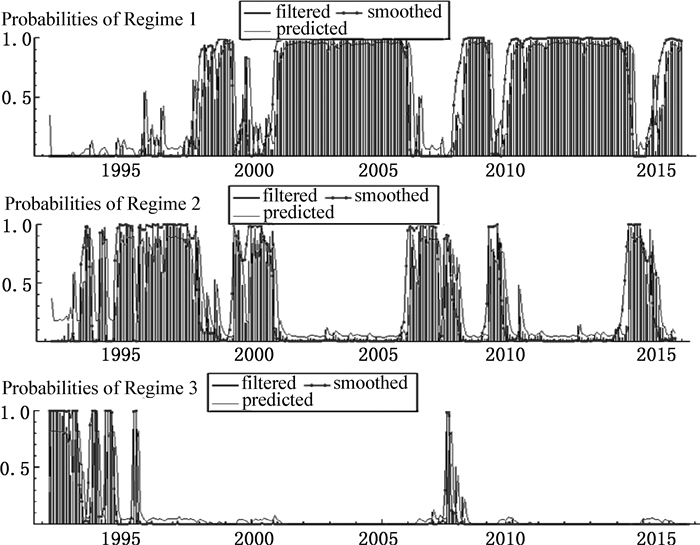
2.区制分类及转换概率分析。本文以1992年1月至2016年10月的月度数据为研究资料,采用MSIH(3)-VAR(3)模型得出区制分类结果,如图 4所示。横轴代表年份,纵轴代表概率值。区制一表示低通胀和较低实际股票收益率,包括1997年下半年至1999年上半年、2001年下半年至2005年上半年、2009年下半年至2010年下半年、2011年至2014年上半年①、2015年下半年至2016年年底,均对应了我国股票市场的熊市和我国自1992年以来经历的5次通货紧缩时间。区制二表示温和通胀和高实际股票收益率,包括1996年至1997年上半年、1999年下半年至2001年上半年、2005年下半年至2007年年底、2010年下半年至2011年上半年、2015年上半年,均对应了我国股票市场发展中的几次牛市并覆盖了我国的两次温和通胀。区制三表示严重通货膨胀和低实际股票收益率,包括1993年年初至1994年下半年、2007年下半年至2008年年底,同样对应了我国股市中的熊市和高通胀的时间。图 4表明,运用MS-VAR非线性模型分析我国实际股票收益率和通胀率的关系是合理并有效的,模型分析结果与实际情况基本一致,也充分说明了通胀率对我国实际股票收益率存在非对称影响以及前文假设的合理性。
|
图 4 三区制平滑概率图 |
此外,运用MSIH(3)-VAR(3)模型还可估计出各个区制的性质,包括所处区间的样本数量、频率和平均持续时间以及各区制间转换的概率,具体结果见表 2。如表 2,经济体更大概率维持自身的状态。区制一状态,即经济体处于低通胀率和较低实际股票收益率状态,持续概率为96.88%,频率为61.27%,平均持续时间为32.05个月,由区制一转换至区制二的概率为3.12%,区制一转换至区制三的概率微乎其微,即由低通胀迅速转换至高通胀的概率几乎为0。由此我们可以得出结论,我国的经济系统大部分时间处于低通胀和低实际股票收益率状态,这也可以充分解释大多数股票投资者不能从股市中获益。区制二状态,即经济体处于温和通胀和高实际股票收益率状态,自身持续概率为89.68%,处于此阶段的频率为31.36%,平均持续时间为9.69个月。区制三状态,即经济体处于高通胀和低实际股票收益率状态,自身持续概率为82.03%,处于此阶段的频率为7.36%,平均持续时间为5.56个月,由区制三转换至区制二的概率为17.97%,远高于其他区制间的转换概率。区制三的平均持续时间以及出现的频率均远小于区制一和区制二,可见,我国的通胀水平一般处于较低水平,即使处于高通胀水平也会迅速转变为温和通胀状态。
| 表 2 三区制描述性统计及转换概率 |
为了进一步深入剖析通胀率与实际股票收益率之间的关系,下文将运用脉冲响应函数和区制转换脉冲响应函数对此开展讨论。
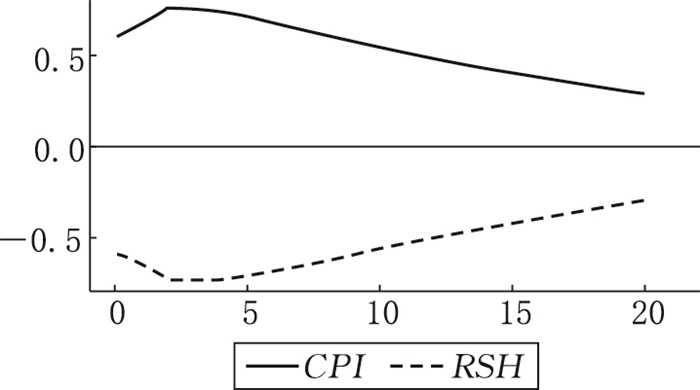
3.脉冲响应函数分析。给定通货膨胀一个标准差的冲击,分析在三区制下股票收益的响应程度,并比较经济体处于不同状态下变量之间短期的动态关系,从而可以进一步揭示通货膨胀率和实际股票收益率之间的伴随关系。详见图 5—7。
|
图 5 区制一状态下的脉冲响应分析 |
|
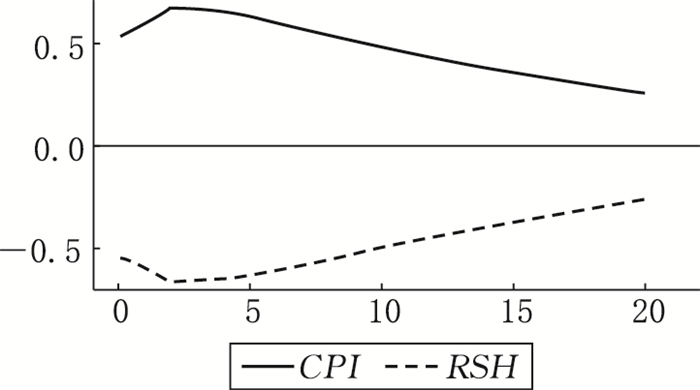
图 6 区制二状态下的脉冲响应分析 |
|
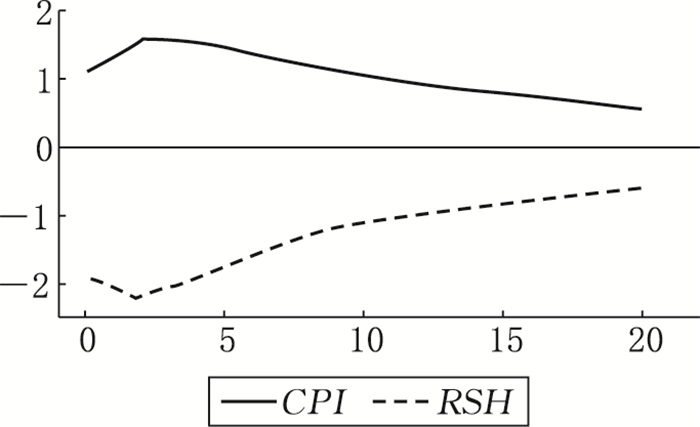
图 7 区制三状态下的脉冲响应分析 |
在区制一(低通胀水平和低实际股票收益率)状态下,如果给定通货膨胀率一个标准差的正向冲击,实际股票收益率在前两个月内保持负的递增,并且在第2个月达到最大负向响应值,随后从第3个月开始负响应逐渐降低,到第20个月的时候逐渐收敛。实际股票收益率没有伴随通胀率的改善而提高,可能的原因是当通胀率非常低时,短期的正向冲击也无法使实际股票收益率上升。在通货紧缩时,消费和投资均处于萎缩状态,消费低迷使得企业产品滞销量增加,产品总供给大于总需求,企业盈利能力下降;同时通货紧缩下实际利率较高,企业融资成本增加,这些因素均会使得股价下跌,股市陷入低迷状态。
在区制二(温和通胀水平和高实际股票收益率)状态下,如果给定通货膨胀率一个标准差的正向冲击,不管是从趋势的角度还是从响应程度大小的角度来看,实际股票收益率的响应均与区制一状态下基本相同。同时从响应结果可以看出,温和通胀时实际股票收益率是最可观的,随着通胀水平进一步提高,极有可能进入高通胀区制内,实际股票收益率会逐渐降低,该脉冲响应结果也充分说明了区制二状态下的实际股票收益率高于区制三状态下的实际股票收益率。
在区制三(高通胀水平和低实际股票收益率)状态下,如果给定通货膨胀率一个标准差的正向冲击,实际股票收益率的响应趋势与区制一、区制二相同,但响应程度明显大于区制一、区制二,股票收益率在第2个月达到最大负响应值后迅速回升,表明在区制三高通胀的状态下,如果通胀率进一步恶化,股市会进入持续的低迷状态甚至会造成股市的暴跌。当通胀率超过一定限度时,央行会迅速出台从紧的货币政策,势必严重阻滞股票价格上涨的动力。
综上所述,我们可以得出以下两点结论:首先,MS-VAR模型的脉冲响应函数可以准确地刻画当通胀率突然降低时,实际股票收益率的响应路径和响应的大小程度。其次,给定通胀率一个正向的外界冲击,短期内会产生负面影响。脉冲响应结果解释了当央行实施从紧的货币政策来抑制物价的快速上涨时,会对股票市场形成一种负面影响,这也是股市中的“利空”因素之一。相关的解释是物价水平会随着货币供应量的变化而变化,货币供应量增加驱动物价上涨,货币供应量减少导致物价降低,投资者会根据上市公司未来的盈利水平进行理性的投资,如果预测公司未来营收有所下滑,作为理性人一定会降低股票的投资占比甚至不再进行股票资产的投资,从而使得实际股票收益率下降。同时,这也说明了我国的股票市场仍然是一种政策导向的市场。
4.区制转换脉冲响应分析。本文在脉冲响应分析的基础上,创新性地采用区制转换脉冲响应函数解释通胀率和实际股票收益率关系的区制转换问题。脉冲响应图的横轴代表冲击发生以后通胀率和实际股票收益率响应的滞后阶段(月度),纵轴体现通胀率和实际股票收益率的响应程度。
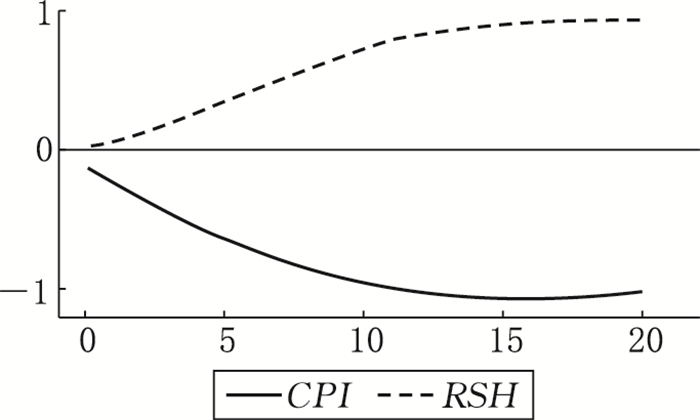
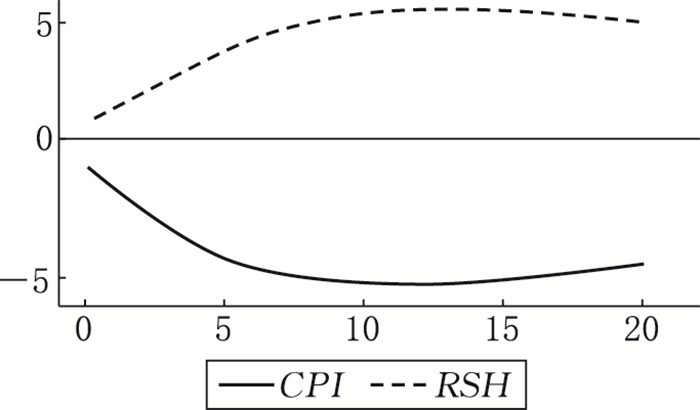
区制一:低通货膨胀率和较低实际股票收益率。如图 8所示,区制一状态下,当经济体受到来自区制内经济变量的冲击时,通胀率与实际股票收益率呈现出负相关的响应关系。当经济系统从区制三转换至区制一时,从图 9看出通货膨胀率呈现出负向递增的响应状态,在第10个月的时候达到最大负值响应;而实际股票收益率则表现为正响应状态,并且在第14个月时达到最大响应值,随后正响应幅度降低,总体而言与通胀率反向变动。由此我们可以得出结论,当从高通胀逐渐恢复至合理的通胀水平时,实际股票收益率有所上升。
|
图 8 变量对区制一内部冲击的响应 |
|
图 9 变量对区制三转换至区制一的响应 |
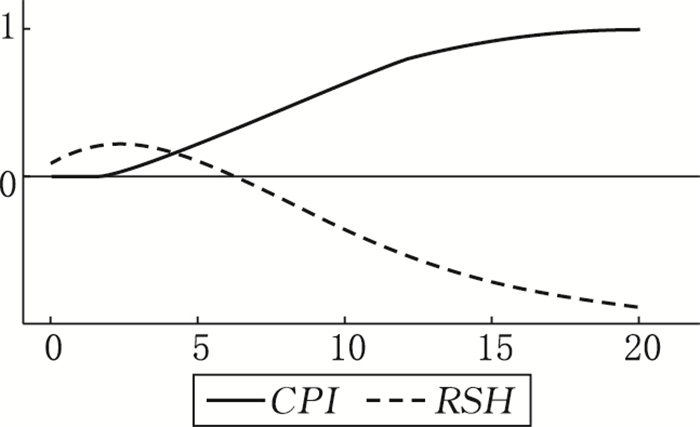
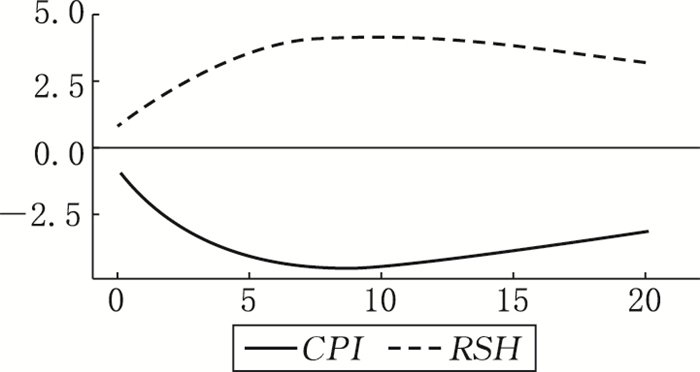
区制二:温和通胀率和高实际股票收益率。如图 10所示,区制二状态下,当经济体受到来自区制内经济变量的冲击时,第1个月和第2个月实际股票收益率呈现出正向的响应,并在第2个月达到最大正响应值,随后逐渐下降,直至第6个月实际股票收益率开始表现出负向的响应。与之不同的是通货膨胀率一直呈现正向的响应。由此可以看出,自冲击发生的当期到第3个月为止,实际股票收益率和通胀率呈现正向变动,而第3个月之后,通货膨胀率和实际股票收益率呈现负相关的响应关系,“费雪效应”不再适用。如图 11所示,当经济系统从区制三转换至区制二时,首先我们可以确定通货膨胀率降低而实际股票收益率上升,其次通货膨胀率呈现负向递增的响应,负向响应程度在第8个月达到最大值,随后负向响应逐渐减少,而实际股票收益率的响应路径与通胀率完全相反,实际股票收益率在第8个月达到最大正响应值,随后正响应幅度逐渐降低。所以当经济系统由区制三转换至区制二时,实际股票收益率和通胀率呈反向变动的关系,“费雪效应”也不适用。
|
图 10 变量对区制二内部冲击的响应 |
|
图 11 变量对区制三转换至区制二的响应 |
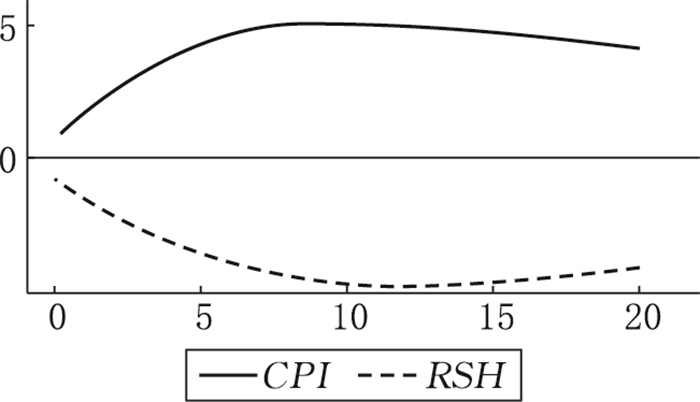
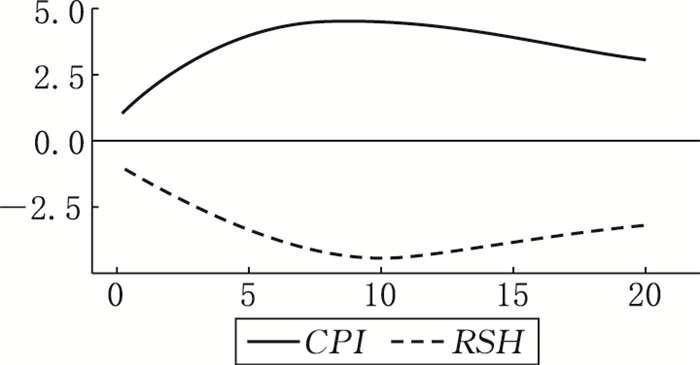
区制三:高通胀率和低实际股票收益率。图 12表明当经济体受到来自区制三内相关经济变量的冲击时,实际股票收益率与通胀率呈现负向变动且两者的响应程度均显著大于区制一下的响应程度,此时“费雪效应”不再适用。经济体从区制一转换至区制三时,其响应如图 13所示,通胀率与实际股票收益率呈负向变动。当货币供应量快速增加时,物价水平会迅速上涨,通货膨胀率也随之上升。通货膨胀率在第9个月时达到正向响应最大值,随后开始轻微下降,主要的原因是利率下降使得实际股票收益率上升,部分资金从商品市场流向股票市场,商品市场供过于求,从而导致物价轻微下跌。经济体从区制二转换至区制三时,其响应如图 14所示,通胀率与实际股票收益率也是呈负向变动,但是响应程度明显低于从区制一转换至区制二的情况,主要是由于区制二与区制三的通胀率水平比较接近,而区制一与区制三的通胀率水平相差较大。
|
图 12 变量对区制三内部冲击的响应 |
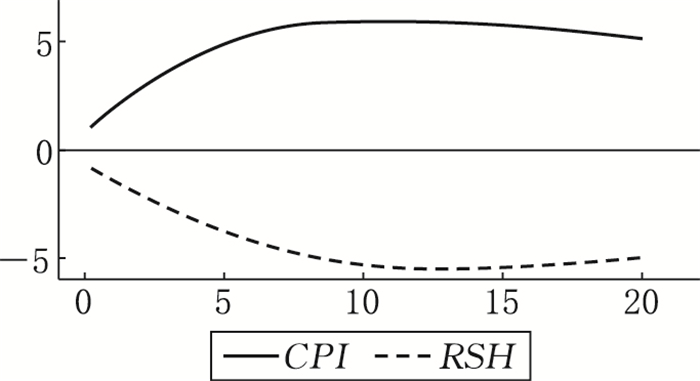
|
图 13 变量对区制一转换至区制三的响应 |
|
图 14 变量对区制二转换至区制三的响应 |
通货膨胀率和实际股票收益率的相关性一直是宏观经济及金融等研究领域的热点问题之一,它们之间的关系被学者称为“股票收益—通货膨胀之谜”。本文应用三区制MS-VAR模型将通胀水平分为低通胀(通货紧缩)、温和通胀和高通胀,为实际股票收益率和通胀率的非对称关系的分析提供了一个全新的角度,研究所得结论如下:第一,1992年1月至2016年10月,我国通胀率和实际股票收益率之间表现为正相关或者负相关的关系,“费雪效应”并不适用于我国A股市场,在高通胀期间,股票资产不能弥补通胀导致的购买力损失,与赵留彦(2016)的研究结论不一致① 。第二,在样本范围内,剔除2014年下半年“杠杠牛”导致的唯一一次“通缩与牛市”并存现象,本文提出的3个假设成立,即当我国通胀率较低时,实际股票收益率偏低;当我国处于温和通货膨胀状态时,实际股票收益率最高;当我国处于高通胀状态时,实际股票收益率最低。第三,我国处于区制一的频率最高,由区制一转换至其他区制的概率很低,由区制三转换至区制二的概率远高于其他区制间的转换概率,由此可见,我国的通胀水平一般处于较低的水平,即使处于高通胀水平也会较快转变为温和通胀状态。第四,MSIH(3)-VAR(3)模型的脉冲响应函数分析的结果证明,给定通胀率一个正向的外部冲击,实际股票收益率在3个区制内均呈现与通胀率负向变动的关系,因此我国A股市场也存在“费雪效应之谜”;区制转换脉冲响应结果表明,通胀率和实际股票收益率在区制间进行转换时,当经济体受到来自区制内经济变量的冲击后,大多数情况下两者之间表现为负向变动的趋势,“费雪效用”假说在我国A股市场不适用。
运用马尔科夫区制转换方法分析中国股市的实际收益率与通货膨胀率之间的非对称性关系,为相关研究提供了很好的视角,本文的研究结果意味着股票市场实际收益率与通胀率之间不是单纯的正相关或者负相关关系,分析两者之间的关系时,有必要考虑通胀率的区制依赖性。从区制转换的实证结果看,我国的股票市场仍然是一种政策导向的市场,当通胀率急剧上升至高通胀时,高通胀会使央行收紧流动性,实际股票收益率会随之下降。纵观2000年以来央行的紧缩性货币政策可以看出:当CPI同比回升到1%左右时,央行会停止宽松的货币政策;当CPI同比超过3%时,央行会实行从紧的货币政策,包括加息、提高存款准备金率等;物价的持续上涨使得通胀水平居高不下时,央行会实行紧缩性货币政策,股市往往也会相应地下跌,加息对金融体系的影响比较深远。
苟小菊、王世雷, 2009, 《通货膨胀率和股票收益率的相关性的实证研究——基于马尔可夫转换模型》, 《北京理工大学学报(社会科学版)》第4期。 |
郭建军, 2008, 《对中国股票市场费雪效应及相关"波动性假说"的检验》, 《上海金融》第11期。 |
韩学红、郑妍妍、伍超明, 2008, 《对我国股票收益率与通货膨胀率关系的解释:1992-2007》, 《金融研究》第4期。 |
刘金全、谢卫东, 2003, 《中国经济增长与通货膨胀的动态相关性》, 《世界经济》第6期。 |
刘金全、马亚男, 2009, 《股票收益率与通货膨胀率的相关性研究——基于对我国经济周期波动过程的考察》, 《吉林大学社会科学学报》第1期。 |
王海维, 2017, 《我国通货膨胀率和股票收益率关系的实证研究——基于MS-VAR模型》, 华东师范大学硕士学位论文。 |
王宇伟、丁慧、盛天翔, 2018, 《股票收益率与通货膨胀预期的动态影响关系研究——基于TVP-VAR-SV模型的实证研究》, 《南开经济研究》第6期。 |
薛福星, 2006, 《中国股票市场中实际收益与通货膨胀的关系》, 《统计与决策》第1期。 |
张兵, 2005, 《基于状态转换方法的中国股市波动研究》, 《金融研究》第3期。 |
赵留彦, 2016, 《股票收益与通货膨胀:中国高通胀时期的实证研究》, 《经济学(季刊)》第2期。 |
Barnes, M., Boyd, J.H. and Smith, B.D., 1999, "Inflation and Asset Returns", European Economic Review, Vol.43, No.4. |
Boamah, M.I., 2017, "Common Stocks and Inflation:An Empirical Analysis of G7 and BRICS", Atlantic Economic Journal, Vol.45, No.2. |
Bodie, Z., 1975, Hedging Against Inflation, Ph. D. Dissertation, Massachusetts Institute of Technology.
|
Cifter, A., 2015, "Stock Returns, Inflation, and Real Activity in Developing Countries:A Markov-Switching Approach", Panoeconomicus, Vol.62, No.1. |
Cornell, B. and French, K.R., 1983, "The Pricing of Stock Index Futures", Journal of Futures Markets, Vol.3, No.1. |
Crosby, M., 2001, "Stock Returns and Inflation", Australian Economic Papers, Vol.40, No.2. |
Fama, E.F., 1981, "Stock Returns, Real Activity, Inflation, and Money", American Economic Review, Vol.71, No.4. |
Fama, E.F. and Schwert, G.W., 1977, "Asset Returns and Inflation", Journal of Financial Economics, Vol.5, No.2. |
Gultekin, N., 1983, "Stock Market Returns and Inflation:Evidence from Other Countries", Journal of Finance, Vol.38, No.1. |
Hess, P. and Lee, B., 1999, "Stock Returns and Inflation with Supply and Demand Disturbances", Review of Financial Studies, Vol.12, No.5. |
Hondroyiannis, G. and Papapetrou, E., 2006, "Stock Returns and Inflation in Greece:A Markov-Switching Approach", Review of Financial Economics, Vol.15, No.1. |
Kaul, G., 1987, "Stock Returns and Inflation:The Role of the Monetary Sector", Journal of Financial Economics, Vol.18, No.2. |
Kolluri, B. and Wahab, M., 2008, "Stock Returns and Expected Inflation: Evidence from an Asymmetric Test Specification", Review of Quantitative Finance and Accounting, Vol.30, No.4.
|
Krolzig, H.M., 2013, "Markov-Switching Vector Autoregressions Modelling, Statistical Inference, and Application to Business Cycle Analysis", Springer Science and Business Media, Vol.454.
|
Liu, Z. and Wang, S., 2017, "Decoding Chinese Stock Market Returns: Three-State Hidden Semi-Markov Model", Pacific-Basin Finance Journal, Vol.44.
|
McMillan, D.G., 2017, "Stock Return Predictability:The Role of Inflation and Threshold Dynamics", International Review of Applied Economics, Vol.31, No.3. |
Modigliani, F. and Cohn, R.A., 1979, "Inflation, Rational Valuation and the Market", Financial Analysts Journal, Vol.35, No.2. |
Nelson, C.R., 1976, "Inflation and Rates of Return on Common Stocks", The Journal of Finance, Vol.31, No.2. |


