一 引言

“中兴休克”和“华为事件”表明，高新技术领域已日益成为世界各国科技竞争的焦点，高新技术进步过程中研发规模和研发效率扮演着重要角色。当今世界正处于第五代网络技术、人工智能与大数据时代，一国如何通过研发创新占据技术制高点愈发重要。然而，经济新常态下我国经济面临结构性下行压力，研发资源投资有限，如何最大程度地提高创新要素质量和优化研发资源配置效率尤为迫切。事实上，我国在经济转型过程中市场摩擦与行政干预频繁，再加上地理区位、市场化水平和土地流转改革差异问题，已严重阻碍过剩劳动力跨地区和跨部门自由流动，技能、非技能劳动与岗位非匹配引发人员失业和研发岗位空缺现象普遍。同期，R&D补贴政策偏向和行政机制低效率，又诱致有限的研发资源分布不均，加剧资源错配和创新产出效率损失。为此，在经济新旧动能转换的关键时期，如何有效抑制甚至消除创新要素错配，成为提高创新效率和推动技术进步迫切需要解决的问题。

De Melo(1977)通过建立一般均衡模型测算要素市场的扭曲程度，开始定量研究要素错配问题。Hsieh和Klenow(2009)以收入层面的全要素生产率(TFP)实际分布相对于理想状态的偏离测算要素错配程度，并采用微观企业数据测度要素错配度，结果表明若无要素流动障碍，中国1998—2005年的年均TFP增长率可提高2%。韩剑和郑秋玲(2014)基于1999—2007年中国工业企业数据库，测算中国地区行业内企业和行业间资源错配水平，发现要素错配分别导致行业内30.25%和行业间4.72%的产出缺口。由于Syrquin(1986)将TFP增长分解成行业TFP增长与要素配置效率，无法解释资源配置不合理成因的问题，陈永伟和胡伟民(2011)通过拓展Syrquin分析框架，结合2001—2007年中国制造业企业数据，将要素配置效率变化进一步分解为要素价格扭曲变动与产出份额变动的贡献，发现制造业内部要素错配导致实际产出与潜在产出间约15%的缺口。Aoki(2012)借鉴Chari等(2002)选择比例税形式表征要素配置扭曲的思路，建立多部门一般均衡模型，对比了不同发达国家的资源错配度。袁志刚和解栋栋(2011)依据Aoki(2008)要素错配的核算方法，探究中国农业与非农部门就业比例失衡表现出的劳动力错配程度及其对TFP的影响，结果表明劳动力的部门间错配导致TFP年平均损失约8%。王林辉和袁礼(2014)结合陈永伟和胡伟民(2011)与Aoki(2012)的资源错配分析框架，构造要素相对流动系数重新衡量要素错配度，关注资本错配造成的全要素生产率损失，结合中国1978—2010年八大产业面板数据开展实证检验，结果表明资本错配引发TFP平均下降2.6%。

问题是，中国为何会出现如此大范围和长时间的要素错配呢？大量研究考察了行政干预(靳来群等，2015；陈林等，2016)、金融市场扭曲(张佩、马弘，2012)、出口贸易(Melitz，2003；宋结焱、施炳展，2014)、产业集聚(季书涵等，2016；肖兴志、李沙沙，2018)、对外投资(白俊红、刘宇英，2018)等因素对资源错配的影响，主要观点是将要素错配归因于不完全竞争市场环境，即行政垄断、制度束缚和经济结构失衡(Hsieh & Klenow，2009；袁志刚、解栋栋，2011；王林辉、高庆昆，2013)，尤其是经济转型过程中渐进式市场化改革诱发的过度行政干预与政策管制(韩剑、郑秋玲，2014)。Brandt等(2013)发现，金融资本往往主要流向效率较低的国有部门。靳来群等(2015)的测算结果表明，1998—2007年所有制差异引发的制造业TFP损失年均保持在200%以上，政府干预易形成资源错配。

截至目前，既有文献已就资源错配问题进行了详尽考察，关注了生产要素错配及其引发的全要素生产率损失，但普遍忽视创新要素领域的错配引发技术创新效率损失的问题。一般地，相对于产品生产活动中的生产要素配置问题，研发活动由于需要更高技能和面对更为复杂的创新环境，要素错配现象可能更为严重。白俊红和卞元超(2016)发现，要素市场扭曲对创新产出效率存在显著影响，这一结论得到相关研究的有力验证(戴魁早、刘友金，2016)。不过，这类文献更多关注单一因素的要素错配问题(李静等，2017；马颖等，2018)，缺乏对创新要素R&D人员与R&D资本的双错配可能引发的创新效率损失研究。基于此，本文将构建不完全市场环境中的多部门一般均衡模型，结合创新要素空间错配指标，利用2009—2017年我国31个省份的研发数据，通过对研发创新效率进行分解，对比评价创新要素空间配置效率，并进一步引入不同类型创新要素解释其空间错配及其差异的成因。本文的边际贡献主要在于：一是将Aoki(2012)的生产要素错配分析框架引入研发活动领域，关注R&D人员和R&D资本空间双错配及其对创新效率的影响，丰富和拓展了生产要素错配问题的研究；二是依据创新要素质量和投入结构将创新要素分类，对比考察不同类型创新要素的空间错配及其创新效率损失的差异性后果。

二 理论框架

本文将Aoki(2012)多部门一般均衡模型引入研发创新活动中，构建研发生产函数，考察研发资本和研发人员空间错配对创新效率的影响。假设经济系统存在n个部门，研发生产n种不同的创新产品，最终产品生产函数为：

$ Y_{t}=F(Y_{1t}, Y_{2t}, …, Y_{nt}) $

(1)

其中，Y_t表示第t期的创新总产出，而Y_it为部门i在第t期的创新产出。将最终创新产品价格标准化为1，创新产品i的价格设为P_it，且假设最终创新产品市场完全竞争，得到∂Y_t/∂Y_it=P_it，Y_t=$ \sum _{i=1}^{n} P_{i t} Y_{i t}$。

将部门i的研发生产函数设定为规模报酬不变的Cobb-Douglas形式：

$ Y_{i t}=A_{i t} H_{i t}^{\alpha_{i}} R_{i t}^{1-\alpha_{i}} $

(2)

其中，H_it为部门i在研发创新活动中的R&D人员投入，R_it表示R&D资本投入，A_it代表创新效率或全要素生产率，α_i∈(0，1)表示R&D人员弹性，1-α_i为R&D资本弹性。

借鉴Chari等(2002)和Aoki(2012)的思路，引入劳动力与资本的比例税τ_Hit和τ_Rit表征地区i的R&D人员与R&D资本的价格扭曲程度，假设R&D人员的工资率为w_t，R&D资本的租金率为r_t，部门i的研发利润最大化问题为：

$ \max\limits_{H_{i t}, R_{i t}} P_{i t} Y_{i t}-\left(1+\tau_{H i t}\right) w_{t} H_{i t}-\left(1+\tau_{R i t}\right) r_{t} R_{i t} $

结合利润最大化的一阶条件可得：

$ \frac{\alpha_{i} P_{i t} Y_{i t}}{H_{i t}}=\left(1+\tau_{H i t}\right) w_{t} ; \quad \frac{\left(1-\alpha_{i}\right) P_{i t} Y_{i t}}{R_{i t}}=\left(1+\tau_{R i t}\right) r_{t} $

(3)

假设经济系统中R&D人员和R&D资本总量外生给定，且满足资源约束条件：

$ H_{t}=\sum _{i=1}^{n} H_{i t} ; \quad R_{t}=\sum _{i=1}^{n} R_{i t} $

以R&D人员错配为例，构造部门i的R&D人员错配度指标。先将部门i实际投入的R&D人员数量表示为：

$ H_{it}=\frac{H_{it}}{\sum _{i=1}^{n} H_{it}} H_{t}=\frac{\frac{\alpha_{i} P_{it} Y_{it}}{\left(1+\tau_{Hit}\right) w_{t}}}{\sum _{i=1}^{n} \frac{\alpha_{i} P_{it} Y_{it}}{\left(1+\tau_{Hit}\right) w_{t}}}=H_t\frac{\frac{\alpha_{i} P_{it} Y_{it}}{\left(1+\tau_{Hit}\right) w_{t} Y_{t}}}{\sum _{i=1}^{n} \frac{\alpha_{it} P_{it} Y_{it}}{\left(1+\tau_{Hit}\right) w_{t} Y_{t}}}=H_t\frac{\frac{\varphi_{it} \alpha_{i}}{\left(1+\tau_{Hit}\right)}}{\sum _{i=1}^{n} \frac{\varphi_{it} \alpha_{i}}{\left(1+\tau_{Hit}\right)}} H_{t} $

(4)

其中，φ_it=P_itY_it/Y_t表示部门i的创新产出份额。当部门i不存在R&D人员错配时，τ_Hit=0，那么R&D人员流动无障碍条件下部门i投入的R&D人员数量为：

$ H_{i t}^{*}=\frac{\varphi_{i t} \alpha_{i}}{\alpha_{t}} H_{t} $

(5)

其中，$ \alpha_{t}=\sum _{i=1}^{n} \varphi_{i t} \alpha_{i}$，表示以各部门创新产出份额为权重的加权平均R&D人员研发弹性。

若以地区代替部门，则以地区i实际分配的R&D人员比重与无错配R&D人员比重的比值，构造R&D人员空间错配系数μ_Hit，表示各地区R&D人员的空间错配度：

$ \mu_{H i t}=\frac{H_{i t} / H_{t}}{H_{i t}^{*} / H_{t}}=\frac{H_{i t} / H_{t}}{\varphi_{i t} \alpha_{i} / \alpha_{t}} $

(6)

μ_Hit>1代表地区i的R&D人员分配过剩，μ_Hit < 1代表地区i的R&D人员分配不足。

同理，构造R&D资本空间错配系数μ_Rit：

$ \mu_{R i t}=\frac{R_{i t} / R_{t}}{R_{i t}^{*} / R_{t}}=\frac{R_{i t} / R_{t}}{\varphi_{i t}\left(1-\alpha_{i}\right) /\left(1-\alpha_{t}\right)} $

(7)

将(6)(7)式代入(2)式替换H_it和R_it，取对数差分可得各地区创新产出增长率：

$ \begin{aligned} \Delta \ln Y_{i t}=& \ln \frac{Y_{i t}}{Y_{i t-1}}=\Delta \ln A_{i t}+\Delta \ln \varphi_{i t}-\alpha_{i} \Delta \ln \alpha_{t}-\left(1-\alpha_{i}\right) \Delta \ln \left(1-\alpha_{t}\right) \\ &+\left(\alpha_{i} \Delta \ln \mu_{H i t}+\left(1-\alpha_{i}\right) \Delta \ln \mu_{R i t}\right)+\left(\alpha_{i} \Delta \ln H_{t}+\left(1-\alpha_{i}\right) \Delta \ln R_{t}\right) \end{aligned} $

(8)

根据中值定理，创新产出增长率可近似表示为所有地区创新产出增长率的加权平均形式：

$ \Delta \ln Y_{t}=\sum _{i=1}^{n} \frac{\partial \ln Y_{t}}{\partial \ln Y_{i t}} \Delta \ln Y_{i t} \cong \sum\limits_{i=1}^{n} \bar{\varphi}_{i t} \Delta \ln Y_{i t} $

(9)

其中，φ_it=(φ_it+φ_it-1)/2。将(8)式代入(9)式，可得到创新总产出增长率分解结果：

$ \Delta \ln Y_{t}=\sum _{i=1}^{n} \bar{\varphi}_{it} \Delta \ln Y_{i t}=\sum _{i=1}^{n} \bar{\varphi}_{i t} \Delta \ln A_{i t}+\sum _{i=1}^{n} \bar{\varphi}_{it} \Delta \ln \varphi_{i t}-\\\bar{\alpha}_{t} \Delta \ln \alpha_{i}-\left(1-\bar{\alpha}_{t}\right) \Delta \ln \left(1-\alpha_{t}\right)\\ +\sum _{i=1}^{n} \bar{\varphi}_{i t}\left(\alpha_{i} \Delta \ln \mu_{H i t}+\left(1-\alpha_{i}\right) \Delta \ln \mu_{R i t}\right)+\bar{\alpha}_{t} \Delta \ln H_{t}+\left(1-\bar{\alpha}_{t}\right) \Delta \ln R_{t} $

(10)

其中，$\bar{\alpha}_{t}=\sum _{i=1}^{n} \bar{\varphi}_{i t} \alpha_{i} $。类比产品生产活动过程中全要素生产率的定义(Christensen, et al., 1973；Caves, et al., 1982；Aoki，2012；袁志刚、解栋栋，2011)，可将研发活动的创新效率AIE定义为排除创新要素投入变动后的创新产出增长率：

$ A I E_{t}=\sum _{i=1}^{n} \bar{\varphi}_{i t} \Delta \ln Y_{i t}-\bar{\alpha}_{t} \Delta \ln H_{t}-\left(1-\bar{\alpha}_{t}\right) \Delta \ln R_{t} $

(11)

结合(10)式和(11)式，可以将创新效率AIE进行分解，结果如(12)式：

$ A I E_{t}=\underbrace{\left(\sum _{i=1}^{n} \bar{\varphi}_{i t} \Delta \ln A_{i t}\right)}_{地区创新效率(SAIE)}+\underbrace{\left(\sum _{i=1}^{n} \bar{\varphi}_{i t} \Delta \ln \varphi_{i t}-\bar{\alpha}_{t} \Delta \ln \alpha_{t}-\left(1-\bar{\alpha}_{t}\right) \Delta \ln \left(1-\alpha_{t}\right)\right)}_{结构效率(SS)}\\ +\underbrace{\left(\sum _{i=1}^{n} \bar{\varphi}_{i t}\left(\alpha_{i} \Delta \ln \mu_{H i t}+\left(1-\alpha_{i}\right) \Delta \ln \mu_{R i t}\right)\right)}_{创新要素空间配置效率(FAE)} $

(12)

由(12)式可知，整体创新效率的变化率可以分解成三部分的贡献结果。第一项记为地区创新效率$ S A I E_{t}=\sum _{i=1}^{n} \bar{\varphi}_{i t} \Delta \ln A_{i t}$，表示地区创新效率变化引起经济整体创新效率的变动。第二项记为结构效率$ S S_{t}=\sum _{i=1}^{n} \bar{\varphi}_{i t} \Delta \ln \varphi_{i t}-\bar{\alpha}_{t} \Delta \ln \alpha_{t}-\left(1-\bar{\alpha}_{t}\right) \Delta \ln \left(1-\alpha_{t}\right)$，表示由于各地区的创新产出份额变化导致整体创新效率的变化。若SS_t>0，则表示创新产出的地区结构趋于合理，有利于提高整体创新效率；反之，则表明创新产出的地区结构失衡而降低整体创新效率。第三项记为创新要素空间配置效率$ F A E_{t}=\sum _{i=1}^{n} \bar{\varphi}_{i t}\left(\alpha_{i} \Delta \ln \mu_{H i t}+\left(1-\alpha_{i}\right) \Delta \ln \mu_{R i t}\right)$，表示各地区创新要素配置状态变动引起整体创新效率的变化。若FAE_t < 0，则表明创新要素空间错配加深，引发创新效率损失，其损失大小即为FAE_t；反之，则表示创新要素配置趋于合理，促进创新效率提高。进一步地，创新要素空间配置效率FAE_t又可以被分解为R&D人员空间配置效率FAE_Ht和R&D资本空间配置效率FAE_Rt：

$ F A E_{H t}=\sum _{i=1}^{n} \bar{\varphi}_{it} \alpha_{i} \Delta \ln \mu_{H it} ; \quad F A E_{R t}=\sum _{i=1}^{n} \bar{\varphi}_{i t}\left(1-\alpha_{i}\right) \Delta \ln \mu_{R i t} $

(13)

为比较各地区创新要素空间配置状态对整体创新效率的影响差异，需要测算特定地区i的创新要素空间配置效率。我们采用Aoki(2012)的做法，将除i地区外的其他地区的下标统一记为-i，假设经济系统中创新要素错配仅仅是由地区i引起的，但是受地区i的影响，其他地区中创新要素同样发生一定扭曲且错配系数相等，统一记为μ_H-it和μ_R-it。以地区i的R&D人员错配为例，测算其对创新效率的影响大小，其中-i地区的R&D人员投入量为：

$ H_{-i t}=H_{t}-H_{i t}=\sum _{k \neq i} H_{k t}=\sum _{k \neq i} \frac{\varphi_{k t} \alpha_{k}}{\alpha_{t}} \mu_{H-i t} H_{t} $

于是，由于i地区R&D人员错配引起的-i地区R&D人员错配的空间错配系数为：

$ \mu_{H-i t}=\frac{H_{-i t} / H_{t}}{\varphi_{-i t} \alpha_{-i t} / \alpha_{t}} $

其中，$\varphi_{-i t}=1-\varphi_{i t}, \alpha_{-i t}=\sum _{k \neq i}\left(\varphi_{k t} \alpha_{k} /\left(1-\varphi_{i t}\right)\right) $。

那么，地区i的R&D人员空间配置效率为：

$ F A E_{H i t}=\bar{\varphi}_{i t} \alpha_{i} \Delta \ln \mu_{H i t}+\bar{\varphi}_{-i t} \bar{\alpha}_{-i t} \Delta \ln \mu_{H-i t} $

(14)

其中，$\bar{\varphi}_{-i t}=1-\bar{\varphi}_{i t}, \bar{\alpha}_{-i t}=\sum _{k \neq i}\left(\bar{\varphi}_{k t} \alpha_{k} /\left(1-\bar{\varphi}_{i t}\right)\right) $。

同理，可得地区i的R&D资本空间配置效率：

$ F A E_{R i t}=\bar{\varphi}_{i t}\left(1-\alpha_{i}\right) \Delta \ln \mu_{R i t}+\bar{\varphi}_{-i t}\left(1-\bar{\alpha}_{-i t}\right) \Delta \ln \mu_{R-i t} $

(15)

其中，$\mu_{R-i t}=\frac{R_{-i t} / R_{t}}{\varphi_{-i t}\left(1-\alpha_{-i t}\right) /\left(1-\alpha_{t}\right)} $，而R_-it=R_t-R_it。

为对比研发创新活动中不同类型创新要素空间配置的差异，将地区i的研发生产函数设定为多类型创新要素投入的Cobb-Douglas形式：

$ Y_{i t}=A_{i t} \prod _{j=1}^{m} H_{i j t}^{\alpha_{i j}} \prod _{j=1}^{m} R_{i j t}^{\beta_{i j}} $

(16)

其中，下标i代表地区；j代表要素类型；t表示年份；Y_it、A_it分别为各地区的创新产出和创新效率；H_ijt、R_ijt、α_ij和β_ij分别表示i地区j类型的R&D人员投入、R&D资本投入、R&D人员研发弹性和R&D资本研发弹性。

假定R&D活动规模报酬不变，即$\sum_{j=1}^{m}\left(\alpha_{i j}+\beta_{i j}\right)=1 $。同理，参照未细分要素类型情况下创新要素空间错配系数测量指标的构造方法，可以得到i地区j类型R&D人员与R&D资本的空间错配系数：

$ \mu_{H i j t}=\frac{H_{i j t} / H_{j t}}{\varphi_{i t} \alpha_{i j} / \alpha_{j t}} ; \quad \mu_{R i j t}=\frac{R_{i j t} / R_{j t}}{\varphi_{i t} \beta_{i j} / \beta_{j t}} $

(17)

其中，$\alpha_{j t}=\sum _{i=1}^{n} \varphi_{i t} \alpha_{i j}, H_{j t}=\sum _{i=1}^{n} H_{i j t}, \beta_{j t}=\sum _{i=1}^{n} \varphi_{i t} \beta_{i j}, R_{j t}=\sum _{i=1}^{n} R_{i j t} $。

此时，经济系统满足资源约束条件：

$ H_{t}=\sum _{j=1}^{m} H_{j t}=\sum _{j=1}^{m} \sum _{i=1}^{n} H_{i jt} ; \quad R_{t}=\sum _{j=1}^{m} R_{j t}=\sum _{j=1}^{m} \sum _{i=1}^{n} R_{i j t} $

同样，假定最终创新产品生产函数Y_t=F(Y_1t，Y_2t，…，Y_nt)规模报酬不变，可得$ \Delta \ln Y_{t} \cong\sum _{i=1}^{n} \bar{\varphi}_{i t} \Delta \ln Y_{i t}$，其中$\bar{\varphi}_{it}=\left(\varphi_{it}+\varphi_{it-1}\right) / 2, \bar{\alpha}_{j t}=\sum _{i=1}^{n} \bar{\varphi}_{it} \alpha_{i j}, \bar{\beta}_{j t}=\sum _{i=1}^{n} \bar{\varphi}_{it} \beta_{i j} $。

结合创新效率AIE的定义(11)式，以及(16)(17)式，创新效率AIE可分解为：

$ A I E_{t}=\underbrace{\left(\sum _{i=1}^{n} \bar{\varphi}_{i t} \Delta \ln A_{i t}\right)}_{地区创新效率(SAIE)}+\underbrace{\sum _{i=1}^{n} \bar{\varphi}_{i t} \Delta \ln \varphi_{i t}-\sum _{j=1}^{m}\left(\bar{\alpha}_{j t} \Delta \ln \alpha_{j t}+\bar{\beta}_{j t} \Delta \ln \beta_{j t}\right)}_{结构效率(SS)}\\ +\underbrace{\left(\sum _{i=1}^{n} \bar{\varphi}_{i t} \sum _{j=1}^{m}\left(\alpha_{i j} \Delta \ln \mu_{H i j t}+\beta_{i j} \Delta \ln \mu_{R i j t}\right)\right)}_{创新要素空间配置效率(FAE)} $

(18)

进一步可将创新要素配置效率FAE分解为R&D人员空间配置效率FAE_Ht和R&D资本空间配置效率FAE_Rt；可将FAE_Ht分解为低、中与高技能R&D人员空间配置效率即FAE_H1t、FAE_H2t与FAE_H3t，FAE_Rt分解为基础研究、应用研究与试验发展R&D资本空间配置效率即FAE_R1t、FAE_R2t与FAE_R3t：

$ F A E_{H t}=F A E_{H1t}+F A E_{H2t}+F A E_{H3t}=\\\underbrace{\sum\limits_{i=1}^{n} \bar{\varphi}_{it} \alpha_{i1} \Delta \ln \mu_{Hi1t}}_{低技能{\rm R\&D}人员配置效率}+\underbrace{\sum\limits_{i=1}^{n} \bar{\varphi}_{i t} \alpha_{i 2} \Delta \ln \mu_{Hi2t}}_{中技能{\rm R\&D}人员配置效率}+\underbrace{\sum\limits_{i=1}^{n} \bar{\varphi}_{i t} \alpha_{i3} \Delta \ln \mu_{Hi3t}}_{高技能{\rm R\&D}人员配置效率} $

(19)

$ F A E_{R t}=F A E_{R1t}+F A E_{R2t}+F A E_{R3t}=\\\underbrace{\sum\limits_{i=1}^{n} \bar{\varphi}_{it} \beta_{i1} \Delta \ln \mu_{Ri1t}}_{基础研究{\rm R\&D}资本配置效率}+\underbrace{\sum\limits_{i=1}^{n} \bar{\varphi}_{i t} \beta_{i 2} \Delta \ln \mu_{Ri2t}}_{应用研究{\rm R\&D}资本配置效率}+\underbrace{\sum\limits_{i=1}^{n} \bar{\varphi}_{i t} \beta_{i3} \Delta \ln \mu_{Ri3t}}_{试验发展{\rm R\&D}资本配置效率} $

(20)

类似地，地区i中j类型R&D人员的空间配置效率：

$ F A E_{H i j t}=\bar{\varphi}_{i t} \alpha_{i j} \Delta \ln \mu_{H i j t}+\bar{\varphi}_{-i t} \bar{\alpha}_{-i j t} \Delta \ln \mu_{H-i jt} $

(21)

其中，$ \bar{\varphi}_{-i t}=1-\bar{\varphi}_{i t}, \bar{\alpha}_{-i j t}=\sum _{k \neq i}\left(\bar{\varphi}_{k t} \alpha_{k j} /\left(1-\bar{\varphi}_{i t}\right)\right), \mu_{H-i j t}=\frac{H_{-i j t} / H_{j t}}{\varphi_{-i t} \alpha_{-i j t} / \alpha_{j t}}$表示i地区j类型R&D人员错配引起的-i地区j类型R&D人员的空间错配程度，$H_{-i j t}=H_{j t}-H_{i j t}, \varphi_{-i t}=1-\varphi_{i t}, \alpha_{-i j t}=\sum _{k \neq i}\left(\varphi_{k t} \alpha_{k j} /\right.\left.\left(1-\varphi_{i t}\right)\right) $。

同理，可得地区i中j类型R&D资本空间配置效率：

$ F A E_{R i j t}=\bar{\varphi}_{it} \beta_{i j} \Delta \ln \mu_{R i j t}+\bar{\varphi}_{-i t} \bar{\beta}_{-i j t} \Delta \ln \mu_{R-i jt} $

(22)

其中，$\bar{\beta}_{-i j t}=\sum _{k \neq i}\left(\bar{\varphi}_{kt} \beta_{k j} /\left(1-\bar{\varphi}_{i t}\right)\right) $, $\mu_{R-i j t}=\frac{R_{-i j t} / R_{j t}}{\varphi_{-i t} \beta_{-i j t} / \beta_{j t}}, R_{-i j t}=R_{j t}-R_{i jt} $, $ \beta_{-i j t}=\sum _{k \neq i}\left(\varphi_{kt} \beta_{k j} /(1\right.\left.\left.-\varphi_{i t}\right)\right)$。

三 指标选取与参数估计 (一) 指标选取

指标选取过程如下：(1)创新产出Y。一般地，创新产出度量可以使用专利申请数、新产品开发数、新产品销售收入。相对专利授权数而言，专利申请数更能反映当期的创新产出结果。基于此，本节将采用专利申请数作为创新产出指标。(2)R&D人员投入S。一般采用R&D人员全时当量表征研发创新活动中的劳动力投入(戴魁早、刘友金，2016；白俊红、卞元超，2016)。(3)R&D资本投入R。R&D资本投入以R&D资本存量表征，R&D资本存量选择永续盘存法进行估算。借鉴美国商务部经济分析局(BEA)关于R&D资本化的测算思路(杨林涛等，2015)，R&D资本存量R_t的递推公式为R_t=$ \left(1-\frac{1}{2} \xi\right) E_{t}+(1-\xi) R_{t-1}$，其中，E_t表示第t期R&D资本实际投资，ξ为R&D资本的折旧率。利用实际数据测算R&D资本存量，需要先确定基期R&D资本存量R₀、当期新增R&D投资额、R&D投资价格指数和折旧率ξ：(1)基期R&D资本存量$ R_{0}=\frac{E_{1}(1-\xi / 2)}{g+\xi}$，其中，E₁表示第1期的R&D投资，g为R&D投资的平均增长率。(2)当期新增R&D投资额。吴延兵(2006)认为由于要素投入划分为研发人员和研发资本，需要从R&D支出中扣除人员劳务费，以此表征当期新增的R&D投资。江永宏和孙凤娥(2016)则依据2008年SNA对R&D支出资本化核算方法的修订，基于R&D经费内部支出调整R&D资产的统计范围。基于分省份数据可得性限制，本文采用扣除人员劳务费的R&D经费内部支出作为新增的R&D投资额。(3)R&D投资价格指数的构造。一些文献采用GDP平减指数或固定资产投资价格指数表征R&D投资价格指数(杨林涛等，2015)。也有文献根据R&D投资的构成，选择多组价格指数的加权平均值作为R&D投资价格指数，如吴延兵(2006)利用原材料购进价格指数和固定资产投资价格指数进行构造，白俊红(2011)将其设定为消费者价格指数与固定资产价格指数的加权平均值，江永宏和孙凤娥(2016)则利用工业生产者购进价格指数、R&D人员工资指数以及设备、工器具购置价格指数进行构造。本文选用工业生产者购进价格指数和固定资产投资价格指数的加权平均值构造R&D投资价格指数。^①(4)折旧率ξ。R&D资本折旧率通常设定为15%(Hall & Mairesse，1995)，但基于研究对象不同，一些文献的设定存在差异。王益烜等(2014)建议将R&D资本折旧率设为10%；王亚菲和王春云(2018)依据建筑等实物资本的折旧率计算方法将折旧率设为20.6%；江永宏和孙凤娥(2016)通过假设仪器设备和其他固定资产的使用寿命分别为15年和30年，取残值率4%，假定资产相对效率以几何方式递减，可得仪器设备和其他固定资产的折旧率分别为19.3%和10.2%。本文借鉴江永宏和孙凤娥(2016)的测算结果，将仪器和设备支出的折旧率设定为19.3%，其他资产性支出的折旧率设定为10.2%，而其他日常性支出的折旧率按照一般经验设定为15%。按照这三类资产支出在R&D投资中所占比例加权平均得到R&D资本折旧率。

(二) 参数估计

由于分省份研发数据限制，采用面板回归方法不能取得较好的R&D人员和R&D资本研发产出弹性估计结果。为此，本节依据生产要素报酬核算方法，测算劳动力和资本的要素报酬，并按照R&D人员与R&D资本各自占总就业人数与资本存量的比例，估算创新要素报酬，最后将创新要素收入份额作为研发弹性的估计结果。R&D人员与R&D资本研发产出弹性的测算过程如下：(1)测算劳动与资本报酬。劳动报酬=职工工资总额+社会保险基金，数据取自《中国劳动统计年鉴》。资本报酬=固定资产折旧+营业利润，数据取自《中国工业统计年鉴》。为消除价格波动因素，借鉴姚毓春等(2014)，采用工业生产者出厂价格指数对劳动和资本报酬进行价格平减转换为实际值。(2)测算R&D人员与R&D资本报酬。劳动投入量由年平均劳动人数表征，数据取自《中国工业统计年鉴》，R&D人员数据取自《中国科技统计年鉴》。由于R&D人员的工资通常高于普通劳动力的工资，我们采用“科学研究和综合技术服务业”职工平均工资与所有职业平均工资的比值校准R&D人员报酬，${\rm R\&D}人员报酬=\frac{{\rm R\&D}人员数}{年平均劳动人数}×劳动报酬×\frac{科学研究和综合技术服务业职工平均工资}{所有职业平均工资}$。资本存量与R&D资本存量通过永续盘存法估算得到，因此${\rm R\&D}资本报酬=\frac{{\rm R\&D}资本存量}{资本存量}×资本报酬 $。(3)测算创新要素研发产出弹性。本文假定研发生产函数为规模报酬不变的C-D生产函数形式，采用R&D人员报酬占R&D人员与资本总报酬的相对比例作为各省份R&D人员研发产出弹性，同理可得R&D资本研发弹性。根据研发产出弹性的估算思路，结合2009—2017年31个省份总体研发数据，可得各省份总体及其分类创新要素研发弹性的估计结果，详见表 1和表 2。

四 创新要素空间错配及其创新效率损失测度 (一) 整体经济体内创新要素空间错配及其创新效率损失

表 3列出了31个省份在代表性年度的R&D人员与R&D资本的空间错配系数。数据显示：整体上伴随时间推进，多数省份R&D人员和R&D资本空间错配得到有效缓解，仅有少数省份创新要素配置状况未得到改善甚至不断恶化，如山东的R&D人员和R&D资本配置过剩程度加深，福建的要素分配不足现象日益严重。东北和西北的多数省份R&D人员与资本错配严重，可能原因是伴随东北振兴和西部大开发的战略实施，这些地区得到国家在财政投入和人才政策方面的倾斜，但其研发创新产出效率有限，易导致创新资源过度拥挤。相反，江苏、浙江、广东等东部沿海省份创新要素相对稀缺，尽管东部沿海地区汇集了大量研发资金，也吸引了大量人才，但与这些地区的创新能力相比，创新要素仍供不应求。中部省份如河南、湖北、湖南等的R&D资本配置较为合理，而R&D人员存在一定程度过剩但逐年趋向合理。

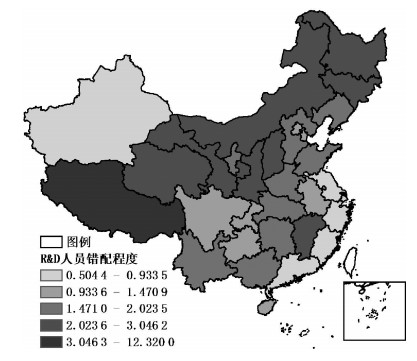
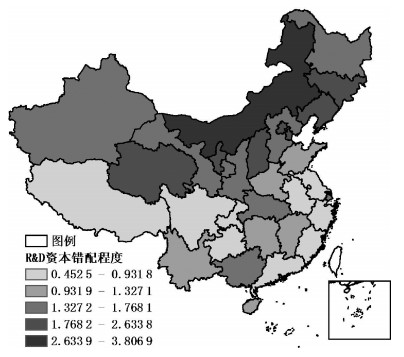
为直观考察不同省份创新要素的空间错配差异，图 1与图 2分别展示了2009—2017年R&D人员与R&D资本平均错配程度空间分布情况。图形显示：总体而言，东部沿海省份的创新要素供给不足，中西部省份存在研发资源配置拥挤现象，并且除四川和重庆外，其他西部省份的要素错配程度更大。对比图 1与图 2，图 1中各省份颜色相对更深，所有省份R&D人员与R&D资本的平均空间错配系数分别为1.967和1.482，表明R&D人员空间错配相较于R&D资本更为严重。

为深入剖析创新要素错配引发的整体创新效率损失情况，根据(12)式可以将整体创新效率AIE分解为地区创新效率SAIE、结构效率SS以及创新要素空间配置效率FAE三项，分解结果见表 4。表 4还计算了创新要素空间配置效率对整体创新效率的贡献率，计算公式为FAE贡献率=100%×|FAE|/(|SAIE|+|SS|+|FAE|)，进而刻画创新要素空间配置状态对整体创新效率变化的解释程度。数据显示：整体创新效率在2010—2017年年均提升5.273%。平均而言地区创新效率SAIE贡献最大，其引起整体创新效率年均提升4.535%；结构效率SS贡献最小，仅导致整体创新效率年均增长0.005%。创新要素空间配置效率FAE对整体创新效率的解释程度平均为7.551%，且创新要素空间错配改善诱使整体创新效率年均提高0.733%。这也表明，创新要素空间错配是引发创新效率损失的重要诱因。此外，可以发现创新要素空间配置效率FAE在样本期间内均大于0，表明创新要素空间配置状态呈现逐年好转趋势，促使整体创新效率不断提升。

进一步根据(13)式，将创新要素空间配置效率FAE分解为R&D人员空间配置效率FAE_H和R&D资本空间配置效率FAE_R，分解结果见表 4最后两行。可以看出，FAE_H和FAE_R在样本期间内均大于0，并且除2012年外，FAE_R均高于FAE_H。平均而言，R&D人员与R&D资本空间错配改善分别使整体创新效率提高0.28%和0.453%。由此得出，R&D人员与R&D资本空间错配均逐年改善，促使整体创新效率不断提升，且R&D资本较R&D人员的错配改善对整体创新效率提升的贡献更大。

根据(14)与(15)式，测算各省份在2009—2017年的平均创新要素空间配置效率，结果见表 5。数据显示：首先，东部沿海省份的创新要素空间配置效率较高，尤其广东的R&D人员配置逐年完善，促使创新效率在2009—2017年年均提高0.0595%，而R&D资本空间配置状态优化引起整体创新效率年均提高0.0837%。原因可能在于，东部沿海省份市场经济自由度和经济发展水平高，创新要素自由流动易促进创新要素得到合理配置。然而，京津沪R&D人员空间配置效率有限，津沪两地R&D人员配置在2009—2017年分别引发整体创新效率平均损失0.0105%和0.0137%。京津沪的经济和科技创新实力强，研发人员和研发资金投入丰裕，但户籍制度限制和高房价在一定程度上仍阻碍科研人员流动，易抑制R&D人员空间配置状态改善。其次，西部省份的R&D人员与R&D资本的空间配置效率相对较小，表明西部省份的创新要素空间错配改善对整体创新效率提升的贡献较小，这可能源于西部地区行政干预频繁且制度不完善，创新要素流动易受阻碍而产生错配。

(二) 分类创新要素空间错配及其创新效率损失

事实上，与多数已有研究类似，前述创新要素空间错配只涉及R&D人员与R&D资本的整体差别，忽略了创新要素质量或投入结构差异可能产生的影响。不同劳动者受教育程度与健康状况不同，劳动质量将存在明显差异，若无差别配置到同一性质岗位则易引发劳动错配。类似地，R&D资本可以投入到不同类型领域，诸如基础研究、应用研究或试验发展活动。通常基础研究投入越多则创新效率可能提升的空间越大，但短期内基础研究无法直接转化生产率。而应用研究或试验发展活动则不同，由于技术研发的直接应用和针对性，在短期内就将对创新效率产生影响。因此，不同研发资本投入结构和长短期投资周期安排都将导致创新效率差异。为此，测算创新要素空间错配及其创新效率损失时，应考虑创新要素的质量或结构差异，否则可能会引发创新要素错配及其效率损失的测算偏误。

基于此，本部分将创新要素分类，考察不同类型创新要素的空间错配，即分别将R&D人员细分为低技能、中技能与高技能等3类^②，以及将R&D资本细分为基础研究、应用研究与试验发展等3类，选择2009—2017年31个省份的分要素类型研发数据，利用(17)式测算低技能、中技能、高技能R&D人员以及基础研究、应用研究、试验发展R&D资本的空间错配度。

表 6列出了各省份低技能、中技能、高技能R&D人员在3个代表性年份的空间错配系数。数据显示：首先，从各省份变化趋势上看，多数省份3类R&D人员的空间错配系数正逐年向1靠近，表明R&D人员的空间配置状态逐渐改善。然而，少数省份3类R&D人员错配均未得到改善甚至反而加剧，如福建短缺现象愈发严重，山东配置过剩程度日益加深，尤其是低技能R&D人员。其次，就全国层面而言，不同类型R&D人员错配存在明显差异，所有省份低技能、中技能、高技能R&D人员的平均错配系数分别为2.050、1.921、1.770，显示出R&D人员技能水平越高则空间错配程度越低。这是源于中低技能R&D人员在劳动力市场中占据较大比例，其从事的研究工作类别繁多、范围广泛，中低技能劳动流动相对更困难且其对政策冲击影响更敏感，而高技能R&D人员质量高、工作专业性强且流动自由度更大，因而相比之下，高技能R&D人员空间错配程度更低。

表 7列出了基础研究、应用研究与试验发展R&D资本在3个代表性年份的空间错配系数。数据显示：首先，多数省份3类R&D资本空间错配系数均不断接近1，表明各类R&D资本的空间错配正逐年缓解。其次，所有省份基础研究、应用研究与试验发展R&D资本的平均错配系数分别为1.236、1.233、1.530，表明平均而言试验发展R&D资本错配更深。由于基础研究和应用研究活动较多发生在高校与研发机构，试验发展活动则主要由企业组织开展，高校与研发机构的专业性强、集中度高，创新要素投入更有针对性，而企业生产的范围广、种类多，出现创新要素误置的概率更大。

根据(18)式，将整体创新效率AIE分解为地区创新效率SAIE、结构效率SS、创新要素空间配置效率FAE等3部分的作用，结果见表 8。对比表 8与表 4发现，未细分与细分要素类型情况下，AIE的分解结果基本一致，其中SAIE最大，SS最小。FAE的影响不可忽视，其平均解释力度达到7.896%，引起整体创新效率年均提升0.756%。这也进一步印证了整体创新效率分解结果的稳健性。继续将FAE分解为R&D人员空间配置效率FAE_H与R&D资本空间配置效率FAE_R，并考虑不同类型创新要素的差异，根据(19)式和(20)式，将FAE_H分解为低技能、中技能与高技能R&D人员空间配置效率即FAE_H1、FAE_H2与FAE_H3，将FAE_R分解为基础研究、应用研究与试验发展R&D资本空间配置效率即FAE_R1、FAE_R2与FAE_R3，具体分解结果见表 8。数据显示：一方面，低技能R&D人员空间配置效率FAE_H1相较中高技能R&D人员空间配置效率更大，试验发展R&D资本空间配置效率FAE_R3相较基础研究与应用研究R&D资本空间配置效率更大。这主要由于低技能R&D人员与试验发展R&D资本在各类创新要素中规模较大，其要素空间错配改善对整体创新效率提升的影响相对较大。另一方面，总体上，R&D人员空间配置效率低于R&D资本空间配置效率，即R&D资本空间错配改善引致整体创新效率的增长率大于R&D人员空间错配改善，这与表 4的结果一致。

为了比较各省份分类创新要素空间配置效率的差异，我们根据(21)(22)式进行了测算。表 9列出31个省份分类创新要素在2009—2017年的平均空间配置效率。数据显示：从整体上看，各省份低技能与中技能R&D人员以及试验发展R&D资本的空间错配对整体创新效率的影响相对而言更大；相较于R&D人员，R&D资本空间错配对整体创新效率的影响更大。具体而言，江苏、浙江、广东的3类R&D人员空间配置状态对整体创新效率的影响相对较大，其中浙江的低技能、中技能与高技能R&D人员空间错配改善分别促使整体创新效率提高0.08165%、0.03150%、0.00106%，而江苏的低技能R&D人员错配加剧引发整体创新效率损失0.02249%。江苏、浙江、广东的3类R&D资本空间配置效率同样较大，而辽宁、北京、吉林等省份的试验发展R&D资本空间配置状态对整体创新效率也会产生重要影响。贵州、宁夏、西藏等省份所有类型创新要素空间配置状态对整体创新效率的影响均较小。

五 基本结论

本文将Aoki(2012)构建的多部门一般均衡模型应用于R&D活动领域，以研发创新生产函数建立创新要素空间错配的理论分析框架，包括构造创新要素空间错配系数和对整体创新效率进行分解，并进一步考察创新要素异质性对错配测算结果的影响，通过将创新要素分类以拓展理论分析，探究不同类型创新要素空间错配之间的差异。本文基于2009—2017年我国31个省份研发数据的实证分析结果发现：(1)未细分与细分创新要素类型情况下的创新效率分解结果均显示，创新要素空间错配改善可促使我国研发创新效率年均提升约0.7%，并且R&D资本错配改善对创新效率提升的影响大于R&D人员错配改善的效果。(2)创新要素空间错配系数的测算结果表明，内蒙古、陕西、青海等西北省份，以及辽宁、吉林等东北省份的创新资源过度拥挤，而江苏、浙江、广东等东部沿海省份对创新要素的需求仍未得到满足。(3)分类创新要素空间错配的测算结果表明，多数省份低技能、中技能和高技能R&D人员以及基础研究、应用研究、试验发展R&D资本的空间错配逐年改善；低技能R&D人员与试验发展R&D资本的空间错配更为严重，并且对整体创新效率的影响相对更大。

基于本文研究结论，政府需要重视：第一，应认识到创新要素的有效配置对创新产出效率提高的重要性，既体现在对研发生产资源的有效利用上，又体现在对提升创新成果质量具有一定促进作用上，因而需要积极推进创新要素市场规范化的建设与发展。第二，应将经济、文化和位置等差异作为地区间分配创新资源的重要考量条件。东部沿海地区资金雄厚、人才密集、城市自由度高、市场制度完善、经济发达，拥有良好的资源环境去实施研发活动，而中西部发展起步较晚，很多基础设施条件、制度环境仍在完善之中，生产能力还未得到充分利用，从而无法将过多精力投入研发创新活动，因此，需要投入更多的创新资源到东部发达地区，以更有效地提高创新产出效率。第三，应重视不同类型创新要素空间错配之间的差异。当前阶段，低技能与中技能R&D人员以及试验发展R&D资本在研发要素总投入中占据相当大的份额，其错配程度对整体创新效率的影响相对而言非常大，且这些类型创新要素的错配程度更高。因此，为了降低创新资源的空间错配程度，需要逐步平衡各类型创新要素的投入比例，进一步提升R&D人员的技能水平，加大对基础研究和应用研究的创新资源投入，从而推动创新成果质量的提升。