过去30多年间,我国推行“一胎化”的计划生育政策,总和生育率(total fertility rate)由原来的约6迅速下降到1.2左右,处于世界上的“超低生育率国家”行列。由于新中国成立后生育“潮”形成的充裕劳动力,“一胎化”的低生育政策并没有阻碍经济增长,反而因有效控制了人口规模而促进了我国人均收入的增长。然而,“一胎化”政策持续30多年,加速了我国人口结构老龄化的进程。根据全国第六次人口普查数据,截至2010年11月1日,我国60岁及以上人口接近1.78亿人,占总人口的13.26%,其中65岁及以上人口占比为8.87%(2012年更是达到9.4%),超过了联合国划定的老龄化标准。
人口结构的老化从人口红利消失和养老资源不足两个方面威胁人口和经济社会的协调发展。有关生育政策、人口结构对经济增长和国民福利的影响,国内存在一些争论。比如,王金营等(2010)通过计量验证了人口红利有力地推动了我国30年来的经济发展。王晶等(2010)从适度人口角度阐述了计划生育政策有利于解决中国人口与现代化发展中的种种矛盾,促进了总体的福利水平。但封进(2004)认为,青年人口增长速度下降会导致社会平均福利下降。蔡昉(2010)对人口红利及刘易斯拐点做了系统的分析,检验并论证得出中国人口红利即将消失。王宇鹏等(2014)利用Ramsey模型分析指出,抚养比的提高对经济发展有正向影响,但会降低社会福利水平。随着老年群体的扩大,老年抚养比大幅上升,养老金短缺问题由此凸显。世界银行公布的一份关于中国未来养老金收支缺口的报告指出,在一定假设条件下按照目前的制度模式,2001年到2075年我国养老保险的收支缺口将高达9.15万亿元。孙博等(2011)实证分析认为,生育率的提高将有效缓解养老金缺口问题。该文指出,逐步放开“二胎”的生育政策,能显著缩小养老金缺口,改善养老金体系财务的可持续性。王桂新(2012)认为,我国的计划生育政策已付出了高昂的经济成本,建议现行的人口与经济发展政策尽快进行调整。
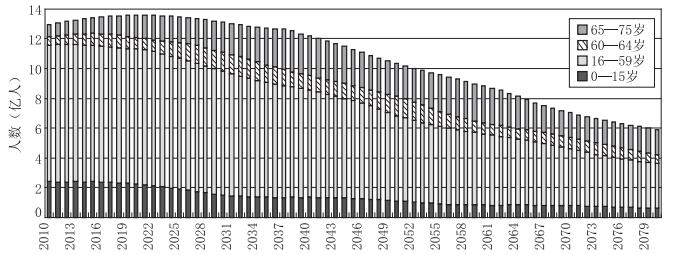
中共十八届三中全会决定启动“单独二胎”政策,但该政策仅使全国每年增加100万左右的新生儿,对人口结构老化的缓解微弱。基于我国第六次人口普查数据,笔者简单地按照25岁的人群“二生一”的生育基数之上再增加100万(代表“单独二胎”的影响)的办法来估算2014年及以后各年的新生儿数,且不考虑死亡率等,最终得到2010—2080年0—75岁人口中分段人口预测数据(见图 1)。结果显示,未来0—15岁和16—59岁年龄段人口数量以及占比处于下降趋势,而60—64岁和65—75岁的人口占比从目前的约10%,上升到10年后的约20%、20年后的25%,30年后达到30%甚至以上。
|
图 1 我国“单独二胎”政策下0—75岁总和与分段人口数量估计(2010—2080年) |
可见,研究进一步放开的人口生育政策势在必行,全面“二胎化”就是一项可供选择的政策。那么,该政策对人口结构和经济福利的作用如何?我国人口生育政策调整对经济增长、居民福利产生影响的机制和效力如何?本文基于世代交叠(OLG)模型,采用1983—2012年省域—跨代合成的面板数据,对此进行理论与实证分析,并对比“单独二胎”政策,分析和预估“全面二胎”政策的作用效果。本文的结论是,我国过去30多年实施的生育政策显著地推动了人均收入的增长,但导致人口的老龄化趋势,带来养老资源不足和老年福利损失的问题。“单独二胎”政策不能从根本上改变人口老龄化的趋势,而全面“二胎化”政策将改善和稳定我国未来的人口结构。因此,我国应立即研究实施全面“二胎化”的生育政策,以稳定劳动力供给和养老、幼教等多方面的需求,并由此助推人口、经济、社会的持续协调发展。
二 基于OLG模型的定性分析借鉴Diamond(1965)给出的世代交叠(Overlapping Generation Model,简称OLG)模型,假定居民一生分为年轻、年老两期。t时期每个年轻人唯一的收入为劳动收入wt,用于满足其当期消费c1, t后储蓄的部分st形成t+1期供1+nt个下一代年轻人(nt是t时期年轻人生育下一代的代际人口增长率)生产中配备的资本(1+nt)kt+1,该资本使用期限为1期(折旧率100%),该资本报酬等于储蓄的本利和(wt-c1, t)(1+rt+1)(其中rt+1为实际利率),并全部为t+1期的每个老年人消费开支所用c2, t+1(消费品为当期产出的一部分)。t时期每个年轻人一生总的消费效用函数为
| $ L=\ln c_{1, t}+\frac{1}{1+\rho} \ln c_{2, t+1}+\lambda\left(w_{t}-c_{1, t}-\frac{1}{1+r_{t+1}} c_{2, t+1}\right) $ | (1) |
求解该最优化问题可得年轻时期、年老时期的消费为:
| $ \left\{\begin{array}{l}{c_{1, t}=\frac{1+\rho}{2+\rho} w_{t}} \\ {c_{2, t+1}=\frac{1+r_{t+1}}{2+\rho} w_{t}}\end{array}\right. $ | (2) |
进而,年轻时期的储蓄为:
| $ s_{t}=w_{t}-c_{1, t}=\frac{w_{t}}{2+\rho} $ | (3) |
设t时期人均形式的生产函数为Atktα。其中,At为当期生产效率,为综合反映当期生产技术、人力资本、制度质量等影响的全要素生产率,可以随时期而改变;小于1的正数α为资本的产出弹性,1-α为劳动的产出弹性。于是,人均形式的生产者利润函数为π=Atktα-(rt+1)kt-wt。求解该利润最大化问题的一阶必要条件是资本的边际产出等于租金率(利率加折旧率),即αAtktα-1=1+rt。人均资本的报酬为(1+rt)kt=αAtktα,而根据欧拉定理(规模报酬固定的生产技术下产出以要素报酬形式分配净尽),工资收入为:
| $ w_{t}=(1-\alpha) A_{t} k_{t}^{\alpha} $ | (4) |
由于t期st形成t+1期资本(1+nt)kt+1,于是由(3)(4)式可得人均资本的动态(差分)方程为:
| $ k_{t+1}=\frac{s_{t}}{1+n_{t}}=\frac{(1-\alpha) A_{t} k_{t}^{\alpha}}{\left(1+n_{t}\right)(2+\rho)} $ | (5) |
在t+1期上述的消费效用最大化和生产利润最大化依次类推,只是把字母下标t换成t+1即可。特别地,在t+1期的生产利润最大化的条件为:
| $ \alpha A_{t+1} k_{t+1}^{\alpha-1}=1+r_{t+1} $ | (6) |
结合(2)(4)(5)(6)式可得t期年轻人在青年、老年时期的消费和终生福利的表达式分别为:
| $ c_{1, t}=\frac{1+\rho}{2+\rho}(1-\alpha) A_{t} k_{t}^{\alpha} $ | (7) |
| $ c_{2, t+1}=\frac{\alpha A_{t+1}\left(1+n_{t}\right)^{1-\alpha}}{(2+\rho)^{\alpha}}\left[(1-\alpha) A_{t} k_{t}^{\alpha}\right]^{\alpha} $ | (8) |
| $ U_{t}=\ln \frac{(1+\rho) \alpha(1-\alpha)^{1+\alpha}\left(1+n_{t}\right)^{1-\alpha} A_{t+1} A_{t}^{1+\alpha} k_{t}^{\alpha(1+\alpha)}}{(2+\rho)^{1+\alpha}} $ | (9) |
从(5)(7)(8)(9)等式可得出如下结论:(1)生产效率At+1提高将促进人均资本的积累和人均产出的增长,提升青年和老年时期的消费水平,并使年轻时单位储蓄换来更高水平的老年期消费。(2)在其他条件不变下,代际人口增长率n的提高,尽管降低下一代人均配备的资本数量而不利于人均收入的增长,但是,其使人口结构年轻化,有利于社会获得更多的养老资源,使年轻时期的储蓄换来更大规模的老年期消费量,促进老年期消费水平的提升,提高终生总的福利水平。
三 省域—跨代的Panel数据分析由于从幼儿到成家立业有20多年的自然成长和接受教育的过程,人口政策和生育率的变动对劳动力数量和经济增长的影响有相应的滞后期,因此,考察人口政策的经济效果,从计量经济学的角度看,样本长度往往难以满足时间序列分析的要求。考虑样本要求和数据可得性,本文采用我国1983—2012年30个省份(重庆①和港澳台除外)的相关数据,合成省域—跨代的面板数据进行实证研究。
(一) 数据与计量方法本文数据来源于中国经济社会发展统计数据库,主要包括各省份统计年鉴(1984—2013年)、《中华人民共和国人口统计资料汇编》(1949—1985年)、《中国统计年鉴》(1984—2013年)、《新中国六十年统计资料汇编》(1949—2008年)等。对有关数据说明如下:(1)人均资本(kt)。由于资本存量数据无法直接获得,因此本文借鉴单豪杰(2008)使用的资本存量估算方法,以1978年为基年得出1983—2012年各省份的资本存量。历年从业人员数据来自于各省份的统计年鉴,进而得出人均资本(实则劳均资本)。(2)全要素生产率(At)。本文使用索洛余值代表全要素生产率,具体估算方法参考叶裕民(2002)。首先,根据索洛经济增长模型计算全要素生产率的增长率:gTFP=gy-αgk-(1-α)gl;然后,计算全要素生产率的水平值。其中,gy为实际经济增长率,本文通过名义GDP增长率扣除CPI的变化率得到;gl为劳动力增长率,选用各地区从业人员数代表劳动力,并计算出其增长率;gk为资本增长率,指标选用资本存量,利用永续盘存法估算出资本存量及其增长率。这里参考了杨再贵(2008),将全国各省份资本要素、劳动要素的产出弹性统一选定为0.35和0.65。(3)代际人口增长率(nt)。本文选用统计年鉴所列各年的出生人口来计算各省份的代际人口增长率。在世代交叠模型中一般选取25年为一期(即25岁工作并生育,50岁退休,75岁的预期寿命)。但考虑到我国《婚姻法》有关结婚年龄的规定、众人对婚育年龄的差异选择,以及就业和退休年龄的差异等因素,本文选取22年、23年、24年、25年共四种代际时间跨度进行分析,希望以此考察数据分析结果的稳健性和可信度。
(二) 实证过程1.单位根检验。为避免变量的不平稳而引起回归方程的参数估计出现偏差,本文采用两种类型的面板数据单位根检验来考察各变量(自然对数值)的平稳性:(1)原假设为相同单位根过程的LIC检验;(2)原假设为个体具有单位根过程的ADF检验和PP检验。由表 1可见,在5%的显著性水平下,ADF检验显示除个别变量外多数变量平稳,LIC检验与PP检验结果显示各变量均平稳。
| 表 1 全国30个省份面板数据各变量的单位根检验结果 |
2.回归模型建立与估计结果。为便于回归,本文将对OLG模型定性分析中的(5)式取自然对数得到:
| $ \ln k_{t+1}=\ln \frac{1-\alpha}{2+\rho}+\ln A_{t}+\alpha \ln k_{t}-\ln \left(1+n_{t}\right) $ | (10) |
为了基于省级面板数据得出全国范围的普遍性结论,而又可体现出各省份的差异,根据(10)式,我们采用变截距的双对数回归模型。具体如下:
| $ \ln k_{t+1}=\lambda+\beta_{2} \ln A_{t}+\beta_{3} \ln k_{t}+\beta_{4} \ln \left(1+n_{t}\right)+\varepsilon $ | (11) |
其中,λ=(λ1,λ2,… λ30)T,ε=(ε1,ε2,… ε30)T。
确立模型估计的形式是建立面板数据模型的关键。使用1983—2012年全国30个省份的面板数据,在F统计量和Hausman检验中,时间跨度为22年时均拒绝了原假设(显著性水平为1%),因此需要建立固定效应模型;而时间跨度为23、24和25年时,检验结果均为接受Hausman检验原假设,拒绝似然比检验原假设,因此,需要建立随机效应模型。Hausman检验和似然比检验的结果如表 2所示。
| 表 2 Hausman检验和似然比检验的具体结果 |
基于以上检验,并为了减少由于截面数据造成的异方差影响,本文使用可行的广义最小二乘估计方法进行估计,结果如表 3所示。
| 表 3 基于省份面板数据的广义最小二乘估计的结果 |
尽管4组回归所采用样本的时间跨度不同,但是,4组回归结果均显示,代际人口增长率、现有人均资本和全要素生产率的影响系数均在1%的显著性水平下显著,且方向一致,与理论模型指示的符号相吻合。这说明上述回归结果具有稳健性和可信性,而且,也验证了OLG模型在我国的适用性。因此,可以采信基于本文回归分析和OLG模型分析的结论。
四 综合分析基于本文第二、第三部分的工作,并将两者结合起来进行综合分析,可得到以下结论:
第一,全要素生产率对人均资本积累、提升青年和老年期消费水平和终生经济福利都具有正向促进作用。比如,代际时间跨度25年的回归显示,全要素生产率每提升1个百分点将使下一代人的劳均资本提升约0.458%。这将进一步促进下一代的人均产出的增长,为后代带来更高的收入和消费福利。
第二,在控制了全要素生产率变动的影响下,代际人口增长率每降低1%,在1%的显著性水平上将使第二代人的人均资本水平提高0.218—2.84个百分点。这说明,过去30年我国限制人口增长的政策有助于人均配备更多的资本,从而对人均收入水平的提升发挥了作用,具有显著的经济增长效应。
不过,必须看到,“一胎化”政策对人均收入的促进作用是在人口结构相对年轻的背景下实现的。在相对年轻的人口结构(如表 4所示,在1982—2007年间,65岁及以上的人口比例为4.9%—8.1%)下,一方面劳动力充足,经济增长享有人口红利;另一方面,社会面临的养老压力小。在我国未来经济增长的人口红利消失而且社会面临愈发沉重的养老压力新的背景下,低生育政策必须及时改变。
| 表 4 老年人口占比及抚养比 |
第三,提升人口出生率,改善人口结构,对增长老年人的消费和改善其经济福利发挥正向的促进作用。具体而言,在不考虑其他因素变动的情况下,由(8)式可得,代际人口增长率每提升一个百分点,单个人老年期的消费水平将提升1-α个百分点:Δln c2, t+1/Δln(1+nt)=1-α。据此分析,在“一胎化”和“单独二胎”(微弱的变动)政策下,生育水平所对应的代际人口增长率约为-50%,如果改行全面“二胎化”的政策,那么,代际人口增长率将变为0(提升约50个百分点),粗略算来,老年期消费水平将提升32.5个百分点(50×0.65,这里沿用劳动的产出弹性1-α=0.65的假设)。
第四,就“二胎化”相比“一胎化”政策的福利变化而言,上述第二点中描述的降低未来人均资本配备所产生的是负面福利影响,而第三点中描述的老年期消费提升所带来的是正向福利效应,两者在(9)式中得到综合的反映。从(9)式出发,通过推导可以获得人口政策调整导致的总福利变化。其中,采用代际时间跨度25年的回归模型给出的相关系数(代际人口增长率每提高1个百分点,导致下代人均资本下降约0.218个百分点),可计算出“二胎化”(n=0)相比“一胎化”(n=-0.5)政策对未来一代个人终生福利水平的提升幅度为0.3960(如采用22、23、24年的代际时间跨度则结果略有变化,分别为0.3831、0.3782和0.3942,都接近0.40水平)。其计算过程为:
| $ \begin{array}{l} {U_{t + 1, n = 0}} - {U_{t + 1, n = - 0.5}} = \ln \frac{{{{(1 + n)}^{1 - \alpha }}k_{t + 1, n}^{\alpha (1 + \alpha)}:n = 0}}{{{{(1 + n)}^{1 - \alpha }}k_{t + 1, n}^{\alpha (1 + \alpha)}:n = - 0.5}}\\ = \ln \frac{{{{(1 - 0.5 \times 0.218)}^{0.35 \times 1.35}}}}{{{{(1 - 0.5)}^{0.5}}}} = 0.3960 \end{array} $ |
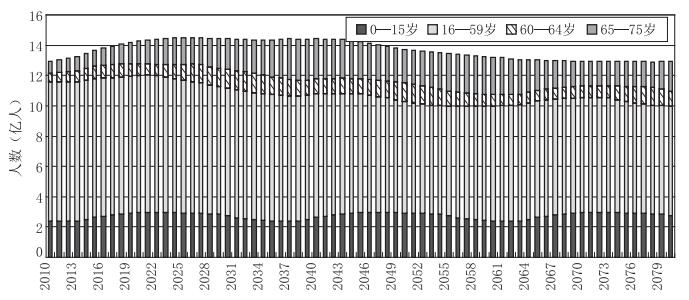
第五,全面“二胎化”政策将改善和稳定我国内地未来的人口结构。相较于图 1描绘的“单独二胎”政策下未来人口结构的老化趋势,图 2描绘了“二胎化”政策对改善和稳定人口结构的积极作用。从中可见,人口结构长期处于相对平稳的发展状态。在这种平稳状态下,劳动力供给和各行业生产稳定,全社会住宅需求、幼托服务和各阶段教育需求、养老服务需求稳定,整个经济体在供给和需求两方面都处于稳定状态,从而有助于人口、经济、社会的持续协调发展。
|
图 2 “二胎化”生育政策下我国大陆0—75岁总和与分年龄段人口数量估计(2010—2080年) |
本文首先运用OLG模型从理论上分析了人口政策和全要素生产率对人均资本和跨期消费的影响,其结果表明:(1)代际人口增长率与人均资本呈反向变动关系,即人口增长不利于人均收入增长;(2)代际人口增长率的上升使得老年期消费增加,有利于提升福利水平;(3)全要素生产率与人均资本、青年期和老年期消费均呈正相关关系。本文利用1983—2012年全国30个省份的面板数据进行实证研究,结果斜率系数的正负与理论模型完全一致,并均在1%的显著性水平下显著,这表明OLG模型在我国的适用性,也说明我国过去30年计划生育政策的实施确实为经济发展与社会福利做出了贡献。
但是,持续30多年的“一胎化”政策使我国正面临人口老龄化的重大挑战,将使未来的经济增长失去劳动力的支持(人口红利消失),也使居民的养老福利受损;而新近开始的“单独二胎”政策作用有限。本文基于2010年人口普查数据进行的未来70年人口变动模拟显示,全面“二胎化”政策将改善和稳定我国内地未来的人口结构,对稳定劳动力供给和养老、幼教等多方面需求起关键作用,并由此助推人口、经济、社会的持续协调发展。
基于理论模型和实证检验进行综合分析的结论显示,如果改行全面“二胎化”的政策,那么,老年期消费水平将提升32.5个百分点,一代人终生的福利水平也将显著提升。因此,本文建议我国应及时研究实施全面“二胎化”的生育政策。
蔡昉, 2010, 《人口转变、人口红利与刘易斯转折点》, 《经济研究》第4期。 |
杜鹏、翟振武、陈卫, 2005, 《中国人口老龄化百年发展趋势》, 《人口研究》第6期。 |
封进, 2004, 《人口结构变动的福利效应:一个包含社会保险的模型及解释》, 《经济科学》第1期。 |
单豪杰, 2008, 《中国资本存量K的再估算:1952—2006年》, 《数量经济技术经济研究》第10期。 |
孙博、董克用、唐远志, 2011, 《生育政策调整对基本养老金缺口的影响研究》, 《人口与经济》第2期。 |
王桂新, 2012, 《生育率下降与计划生育政策的作用:对我国实行计划生育政策的认识与思考》, 《南京社会科学》第10期。 |
王金营、杨磊, 2010, 《中国人口转变、人口红利与经济增长的实证》, 《人口学刊》第5期。 |
王晶、师吉, 2010, 《论计划生育政策对实现福利适度人口的意义》, 《人口学刊》第1期。 |
王宇鹏、王育森, 2014, 《人口年龄结构、经济增长与社会福利:一个"人口红利"的理论分析框架》, 《经济经纬》第3期。 |
杨再贵, 2008, 《企业职工基本养老保险、养老金替代率和人口增长率》, 《统计研究》第5期。 |
叶裕民, 2002, 《全国及各省区市全要素生产率的计算和分析》, 《经济学家》第3期。 |
Diamond, P., 1965, "National Debt in a Neoclassical Growth Model", American Economic Review, Vol.55, No.5(Dec.).
|